Cho hình bình hành ABCD và đường thẳng xy không có điểm chung với hình bình hành. Gọi là các đường vuông góc kẻ từ A, B, C, D đến đường thẳng xy.
Tìm mối liên hệ độ dài giữa AA', BB', CC', DD'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 8 2019
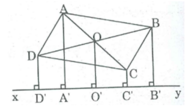
Gọi O là giao điểm của AC và BD
⇒ OA = OC, OB = OD (tính chất hình bình hành)
Kẻ OO' ⊥ xy
AA' ⊥ xy (gt)
CC' ⊥ xy (gt)
Suy ra: AA' // OO' // CC'
Tứ giác ACC'A' là hình thang có:
OA = OC (chứng minh trên)
OO' // AA' nên OO' là đường trung bình của hình thang ACC'A'.
⇒ OO' = (AA' + CC') / 2 (t/chất đường trung bình của hình thang) (1)
BB' ⊥ xy
DD' ⊥ xy (gt)
OO' ⊥ xy (gt)
Suy ra: BB'// OO' // DD'
Tứ giác BDD'B' là hình thang có:
OB = OD (Chứng minh trên)
OO' // BB' nên OO' là đường trung bình của hình thang BDD'B'.
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung bình của hình thang) (2)
Từ (1) và (2) => AA' + CC' = BB + DD'
24 tháng 10 2018
Gọi O là giao điểm của AC và BD .
Kẻ \(OO'\perp xy\)
Ta co : ABCD là hình bình hành có O là giao điểm của 2 đường chéo AC và BD .
=> O là trung điểm của AC và BD
Lại có : \(DD'//AA'//OO'//CC'//BB'\)( cùng vuông góc với xy )
=> CC'AA' và DD'BB' là hình thang .
Xét hình thang CC'AA' ta có :
\(\hept{\begin{cases}OA=OA\\CC'//OO'//AA'\left(cmt\right)\end{cases}}\)( t/c hbh )
\(\Rightarrow OO'=\frac{CC'+AA'}{2}\) (1)
Xét hình thang DD'BB' ta có :
\(\hept{\begin{cases}OB=OD\\DD'//OO'//BB'\left(cmt\right)\end{cases}}\)
\(\Rightarrow OO'=\frac{BB'+DD'}{2}\) (2)
Từ (1) và (2)
=> ...
5 tháng 11 2014
(hình bạn tự vẽ nha)CM:
- gọi giao điểm của hai đường chéo là O
- mà tứ giác ABCD là hình bình hành(gt)
- =>\(OA=OC=\frac{1}{2}ACvàOD=OB=\frac{1}{2}BD\)
- kẻ OO' vuông góc với d
- ta có:OO',AA',BB',CC',DD' vuông góc với d nên OO',AA',BB',CC',DD' song song với nhau
cm OO' là đường trung bình của hình thang BB'D'D=>\(OO'=\frac{BB'+DD'}{2}\left(1\right)\)
- chứng minh OO' là đường trung bình của hình thang AA'C'C=>\(OO'=\frac{AA'+CC'}{2}\left(2\right)\)
- từ (1) và (2)=>\(\frac{AA'+CC'}{2}=\frac{BB'+DD'}{2}\Rightarrow AA'+CC'=BB'+D'D\)
CM
3 tháng 9 2017
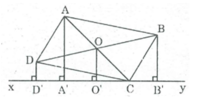
Gọi O là giao điểm của hai đường chéo AC và BD.
Kẻ OO' ⊥ xy
Ta có: BB' ⊥ xy (gt)
DD' ⊥ xy (gt)
Suy ra: BB // OO' // DD'
Tứ giác BB'D'D là hình thang .
OB = OD (t/chất hình bình hành)
Nên O'B' = O'D'
Do đó OO' là đường trung bình của hình thang BB'D'D
⇒ OO' = (BB' + DD') / 2 (tính chất đường trung hình hình thang) (1)
AA' ⊥ xy (gt)
OO' ⊥ xy (theo cách vẽ)
Suy ra: AA' // OO'
Trong ∆ ACA' tacó: OA = OC (tính chất hình bình hành)
OO' // AA' nên OO' là đường trung bình của ∆ ACA'
⇒ OO' = 1/2 AA' (tính chất đường trung bình của tam giác)
⇒ AA' = 2OO' (2)
Tử (1) và (2) suy ra: AA' = BB' + DD'
ko cần vẽ hình đâu nhá