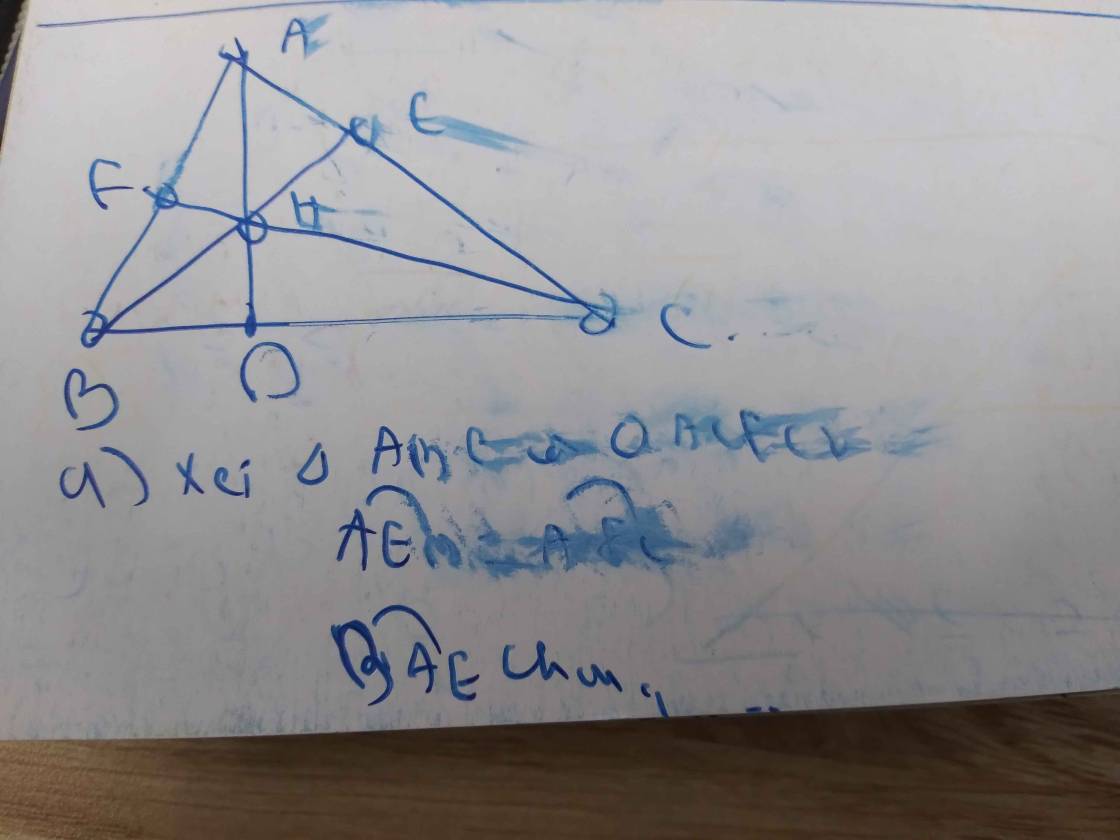
Cho tam giác nhọn ABC có ba đường cao AD, BE và CF cắt nhau tại H.
a)Chứng minh: ∆ABE ∽ ∆ACF, từ đó suy ra AB.AF = AC.AE.
b) Chứng minh: DB . DC = DA.DH
c) Gọi I là trung điểm của BC. Đường thẳng vuông hóc với IH tại H cắt AB và AC lần lượt tại M và N. Chứng minh: ∆AHN ∽ ∆BIH và H là trung điểm của MN.
P/s: mình chỉ còn câu c nữa thôi


c) + \(\left\{{}\begin{matrix}\widehat{BHI}+\widehat{BHM}=90^o\\\widehat{ANH}+\widehat{NHE}=90^o\end{matrix}\right.\)
\(\Rightarrow\widehat{BHI}=\widehat{ANH}\) \(\) ( do \(\widehat{BHM}=\widehat{NHE}\) )
+ \(\left\{{}\begin{matrix}\widehat{HBI}+\widehat{BCE}=90^o\\\widehat{DAC}+\widehat{BCE}=90^o\end{matrix}\right.\)
\(\Rightarrow\widehat{HBI}=\widehat{DAC}\)
+ ΔAHN ∼ ΔBIH ( g.g )
\(\Rightarrow\frac{HN}{IH}=\frac{AH}{BI}=\frac{AH}{CI}\)
+ Tương tự ta cm đc :
ΔAHM ∼ ΔCIH ( g.g )
\(\Rightarrow\frac{HM}{IH}=\frac{AH}{CI}=\frac{HN}{HI}\)
=> HM = HN
=> đpcm