Một người chạy trên dốc có độ dài AC=10m. Biết đỉnh dốc đó cao 4m. Tính khoảng cách từ A đến B( làm trong kết quả đến hàng đơn vị
Cần lời giải gấp ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi: AB là độ cao con đê
BC là đoạn lên dốc của con đê
AC là khoảng cách từ chân dốc đến chân đê
Xét tg ABC vuông tại A, có:
\(BC^2=AB^2+AC^2\left(Pytago\right)\)
\(=>AC^2=BC^2-AB^2\)
\(=>AC=\sqrt{BC^2-AB^2}=\sqrt{8,5^2-4^2}=7,5\left(m\right)\)
Vậy............

Cái này hình như là toán nâng cao , nên mình ko giải được !

Bài 1 :
\(t=30p=1800s\)
\(A=40J\)
Công của người đó đi trong 30 phút là :
\(A=A'.3600=40.3600=144000\left(J\right)\)
Công suất của người đó là:
\(P=\dfrac{A}{t}=\dfrac{144000}{1800}=80\left(W\right)\)
Bài 2 :
Trọng người của người và xe là :
\(p=65.10=650N\)
Lực ma sát: \(F_{ms}=20N\)
Vậy công suất hao phí : \(A_1=F_{ms}.l=20.40=800J\)
Công suất có ích : \(A_2=p.h=650.4=2600J\)
Công suất người sinh ra là : \(A=A_1+A_2=2600+800=3400\left(J\right)\)

Gọi x (km) là độ dài đoạn đường xuống lên dốc (đk: x > 0)
=> độ dài đoạn đường xuống đốc là: 2x (km)
=> Quãng đường AB dài: x + 2x = 3x (km)
Thời gian người đi bộ lên dốc là: \(\frac{x}{2}\) (h)
Thời gian người đi bộ xuống dốc là: \(\frac{2x}{5}\)(h)
Do tổng thời gian đi từ A đến B là 1h48ph = 1,8 (h)
=> Ta có: \(\frac{x}{2}+\frac{2x}{5}=1,8\)
<=> \(x\times\frac{9}{10}=1,8\) => x = 2
=> Quãng đường AB dài: 2 x 3 = 6 (km)

a. Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
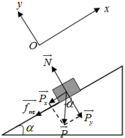
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a →
Chiếu Ox ta có − P x − f m s = m a
⇒ − P sin α − μ N = m a ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1) ⇒ − P sin α − μ P cos α = m a
⇒ a = − g sin α − μ g cos α
Mà sin α = 30 50 = 3 5 ; cos α = 50 2 − 30 2 50 = 4 5
⇒ a = − 10. 3 5 − 0 , 25.10. 4 5 = − 8 m / s 2
Khi lên tới đỉnh dốc thì v = 0 m / s ta có
v 2 − v 0 2 = 2 a s ⇒ 0 2 − v 0 2 = 2. − 8 .50 ⇒ v 0 = 20 2 m / s
b. Khi lên đỉnh dốc thì vật tụt dốc ta có: Chọn hệ quy chiếu Oxy như hình vẽ, chiều dương là chiều chuyển động
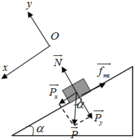
Vật chịu tác dụng của các lực N → ; P → ; f → m s
Theo định luật II newton ta có: N → + P → + f → m s = m a → 1
Chiếu Ox ta có: P x − f m s = m a 1
⇒ P sin α − μ N = m a 1 ( 1 )
Chiếu Oy: N = P y = P cos α ( 2 )
Thay (2) vào (1)
⇒ P sin α − μ P cos α = m a 1 ⇒ a 1 = g sin α − μ g cos α
⇒ a 1 = 10. 3 5 − 0 , 25.10. 4 5 = 4 m / s 2
Áp dụng công thức
v 2 2 − v 2 = 2 a 1 s ⇒ v 2 = 2. a 1 . s = 2.4.0 , 5 = 2 m / s
Thời gian vật lên dốc
v = v 0 + a t 1 ⇒ t 1 = − v 0 a = − 20 2 − 8 = 5 2 2 s
Thời gian xuống dốc
v 2 = v + a 1 t 2 ⇒ t 2 = v 2 a 1 = 2 4 = 0 , 5 s
Thời gian chuyển động kể từ khi bắt đầu lên dốc cho đến khi xuống đến chân dốc : t = t 1 + t 2 = 5 2 2 + 0 , 5 = 4 , 04 s

| \(\sqrt{\sqrt[]{}\frac{ }{ }\hept{\begin{cases}\\\end{cases}}\hept{\begin{cases}\\\\\end{cases}}\orbr{\begin{cases}\\\end{cases}}^{ }^2_{ }}\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| &nbs
|
#)Giải :
Các cạnh AC;AB;BC tạo thành một tam giác
Dựa theo định lí Py - ta - go :
AC2 = BC2 + AB2
=> AB2 = AC2 - BC2
AB2 = 102 - 42
= 100 - 16
AB = \(\sqrt{84}\)= 9,16515139...... \(\approx\)= 9
Vậy : khoảng cách từ A đến B = 9
#) Chúc bn học tốt :D