![]()
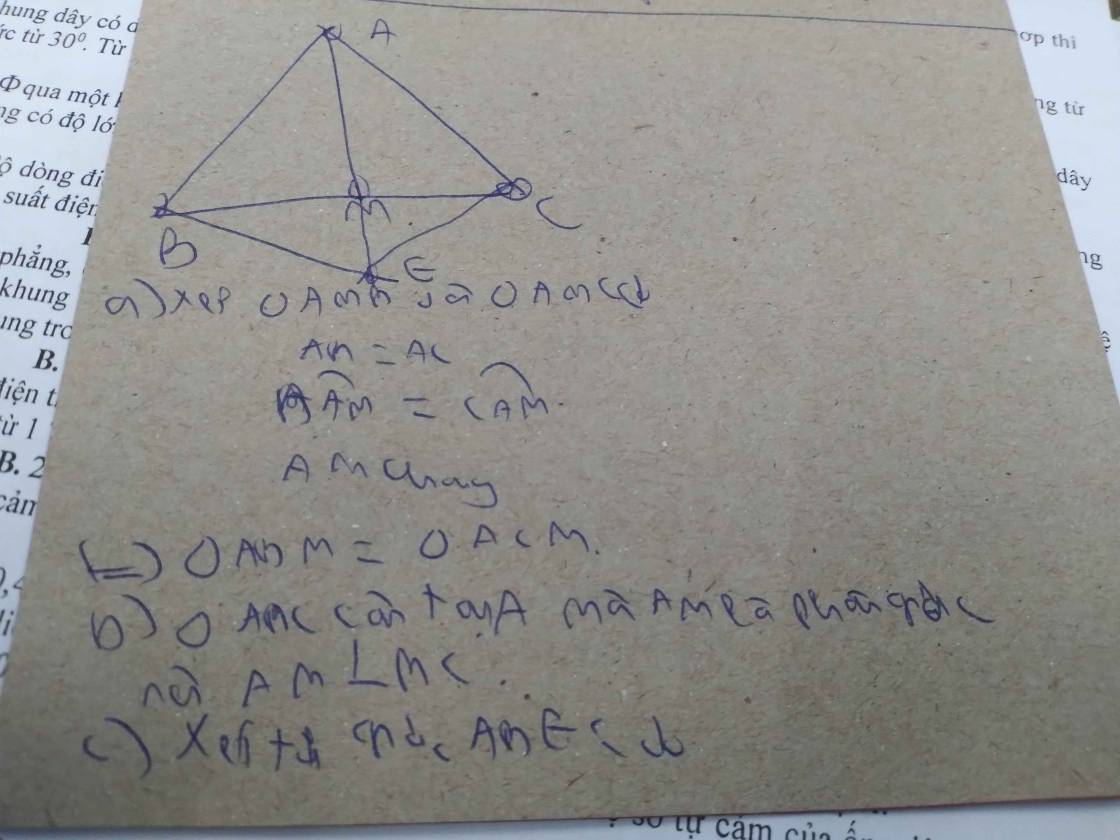
Cho tam giác ABC vuông tại A, có AB=5cm, AC=12cm. Vẽ trung tuyến AM của tam giác ABC
a) Tính độ dài BC.So sánh góc BAM và góc AMB
b) Trên tia đối của tia MA lấy điểm K sao cho MK=MA.Chứng minh tam giác MKC= tam giác MAB
c) chứng minh KC vuông góc với AC


a, tam giác ABC vuông tại A (gt)
=> AB^2 + AC^2 = BC^2 (định lí Pytago)
mà AB = 5 cm; AC = 12 cm (gt)
=> 5^2 + 12^2 = BC^2
=> 25 + 144 = BC^2
=> BC^2 = 169
=> BC = 13 do BC > 0