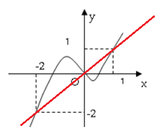
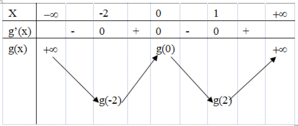
Hàm số y=f(x) có đạo hàm thỏa mãn y=f'(x) ≥ 0 ∀ x ∈ (1;4); f'(x) = 0 ⇔ x ∈ [2;3]. Mệnh đề nào dưới đây sai ?
A. Hàm số f(x) đồng biến trên khoảng (1;2).
B. Hàm số f(x) đồng biến trên khoảng (3;4).
C. f(\(\sqrt{5}\)) = f(\(\sqrt{7}\)).
D. Hàm số f(x) đồng biến trên khoảng (1;4).

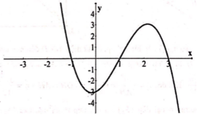
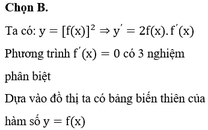
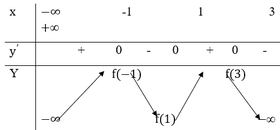


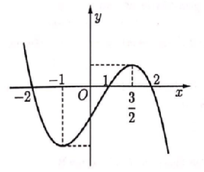
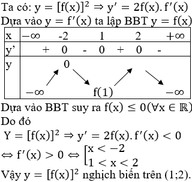
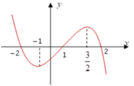
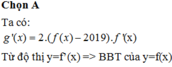
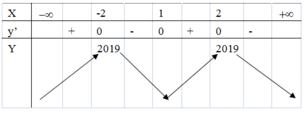
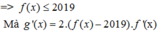
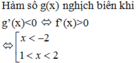
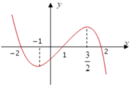
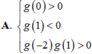
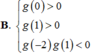
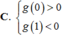
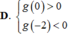






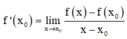 (nếu tồn tại giới hạn).
(nếu tồn tại giới hạn).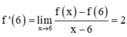
Vấn đề là có đúng 1 câu C đúng, còn lại sai hết =))
\(f'\left(x\right)\ge0\) \(\forall x\in\left(1;4\right)\) thì không có gì đảm bảo rằng khả năng \(f'\left(x\right)=0\) \(\forall x\in\left(1;4\right)\) không xảy ra cả, nó vẫn xảy ra như thường
\(f\left(x\right)\) đồng biến trên \(\left(a;b\right)\) thì \(f'\left(x\right)\ge0\) \(\forall x\in\left(a;b\right)\), đây là một khẳng định đúng
\(f'\left(x\right)\ge0\) \(\forall x\in\left(a;b\right)\) thì \(f\left(x\right)\) đồng biến trên \(\left(a;b\right)\), đây là một khẳng định sai
Khẳng định đúng phải là: \(f'\left(x\right)\ge0\) \(\forall x\in\left(a;b\right)\) và dấu bằng xảy ra tại hữu hạn điểm thì \(f\left(x\right)\) đồng biến trên \(\left(a;b\right)\)
Đề bài ko hề có đoạn quan trọng nhất "bằng 0 tại hữu hạn điểm" nên cả A, B, D đều sai :(