Cho hình vuông ABCD cạnh a . Tìm tập hợp M sao cho :
2 MA2 + MB2 = MC2 + MD2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 5 2018
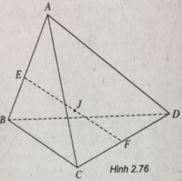
Gọi E, F lần lượt là trung điểm của AB và CD. Ta có:
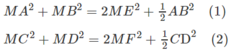
Cộng (1) và (2) ta có:
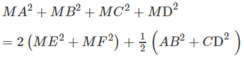
Gọi J là trung điểm của EF, ta có:
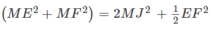
Khi đó:
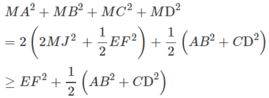
Vậy M A 2 + M B 2 + M C 2 + M D 2 đạt giá trị nhỏ nhất khi M ≡ J.
CM
23 tháng 2 2017
Đáp án D
Với tứ diện đều ABCD thì mặt cầu (S) là mặt cầu có tâm trùng với tâm của mặt cầu ngoại tiếp tứ diện ABCD và là trọng tâm của tứ diện đều cạnh a, đồng thời có bán kính R = a 2 4
Gọi G là trọng tâm của tứ diện ⇒ G A ¯ + G B ¯ + G C ¯ + G D ¯ = 0 ¯
Ta có:
T = M A 2 + M B 2 + M C 2 + M D 2 = M G ¯ + G A ¯ 2 + M G ¯ + G B ¯ 2 + M G ¯ + G C ¯ 2 + M G ¯ + G D ¯ 2
= 4 M G 2 + 2 M G ¯ G A ¯ + G B ¯ + G C ¯ + G D ¯ ⏟ 0 + G A 2 + G B 2 + G C 2 + G D 2 = 4 M G 2 + 4 G A 2
= 4 a 2 4 2 + 4 a 6 4 2 = 2 a 2 . Vậy T = M A 2 + M B 2 + M C 2 + M D 2 = 2 a 2
PT
1
CM
5 tháng 7 2017
Gọi M(x, y)
⇒ MA2 = (x – 1)2 + (y – 2)2
MB2 = (x + 3)2 + (y – 1)2
MC2 = (x – 4)2 + (y + 2)2
MA2 + MB2 = MC2
⇔ (x – 1)2 + (y – 2)2 + (x + 3)2 + (y – 1)2 = (x – 4)2 + (y + 2)2
⇔ [(x – 1)2 + (x + 3)2 – (x – 4)2] + [(y – 2)2 + (y – 1)2 – (y + 2)2] = 0
⇔ (x2 – 2x +1 +x2 + 6x + 9 – x2 + 8x -16) + (y2 – 4y + 4 + y2 – 2y + 1 – y2 – 4y – 4) = 0
⇔ (x2 + 12x – 6) + (y2 – 10y + 1) = 0
⇔ (x2 + 12x – 6 +42) + (y2 – 10y + 1+ 24) = 42 +24
⇔ (x2 + 12x + 36) + (y2 – 10y + 25) = 66
⇔ (x + 6)2 + (y – 5)2 = 66.
Vậy tập hợp các điểm M là đường tròn tâm I(–6; 5), bán kính R = √66.
