Hình 22 cho biết a // b và A4 = 37'( độ )
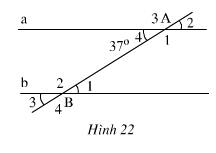
a) Tính B1
b) So sánh A1 và B4
c) Tính B2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a. \(A_4=B_2=37^0\left(slt\right)\)
b. \(A_1=B_1\left(dongvi\right)\)
c. \(B_3=180^0-B_2=180^0-37^0=143^0\left(kebu\right)\)

Do a // b nên ta có:
\(\widehat{A_1}=\widehat{A_3}=54^0(đối đỉnh)\)
\(\widehat{A_3}+\widehat{A_2}=180^0\)
\(\Rightarrow\)\(\widehat{A_2}=180^0-54^0=126^0\)
a)\(\widehat{B_2}=\widehat{A_3}=54^0(đồng vị)\)
b)\(\widehat{A_2}=\widehat{A_4}=126^0(đối đỉnh)\)
\(\Rightarrow\)\(\widehat{A_4}=\widehat{B_3}=126^0(đồng vị)\)
\(\widehat{A_1}<\widehat{B_3}(54^0<126^0)\)
c)\(\widehat{A_4}+\widehat{B_2}=126^0+54^0=180^0\)
a, a//b \(\Rightarrow\widehat{A_4}=\widehat{B_1}=37^0\left(so.le.trong\right)\)
b, a//b \(\Rightarrow\widehat{A_1}=\widehat{B_4}\left(đồng.vị\right)\)
c, \(\widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{B_2}=180^0-37^0=143^0\)
a) Ta có: a//b
⇒A4=B1=370(so le trong)
b) Ta thấy a//b
A1 và B4 là 2 góc đồng vị
⇒A1=B4
c) Ta lại có: A4+B2=1800(trong cùng phía)
⇒370+B2=1800
⇒B2=1800-370=1430