Question

[Bảo Việt]

Gọi d là đườmg thẳng tùy ý đi qua điểm M(1;1) và có hệ số góc âm. Giả sử d cắt các trục Ox, Oy lần lượt tại A, B. Quay tam giác OAB quanh trục Oy thu được một khối tròn xoay có thể tích V. Giá trị nhỏ nhất của V bằng

A. 3\(\pi\)

B.\(\frac{9\pi}{4}\)

C.2\(\pi\)

D.\(\frac{5\pi}{2}\)

Answer 1

[Nguyễn Việt Lâm]

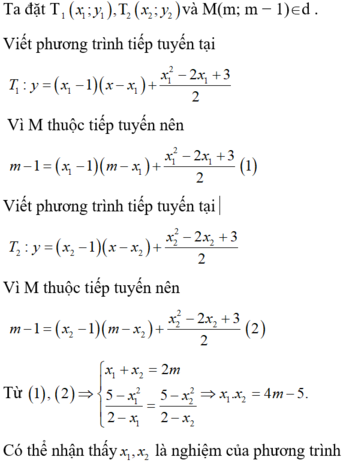
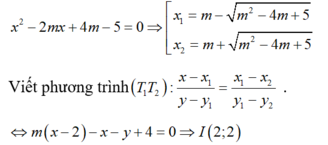
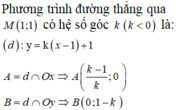
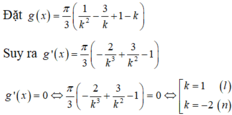
Gọi \(d:\) \(y=ax+b\Rightarrow1=a.+b\Rightarrow b=1-a\Rightarrow y=ax+1-a\) (a<0)

\(\Rightarrow A\left(\frac{a-1}{a};0\right)\); \(B\left(0;1-a\right)\)

Khi quay OAB quanh Oy sẽ thu được khối nón tròn xoay có bán kính đáy \(R=\left|y_B\right|=\left|1-a\right|=1-a\), chiều cao \(h=\left|x_A\right|=\left|\frac{a-1}{a}\right|=\frac{a-1}{a}\)

Thể tích nón: \(V=\frac{1}{3}\pi R^2h=\frac{1}{3}\pi\left(1-a\right)^2.\frac{\left(a-1\right)}{a}=\frac{\pi\left(a-1\right)^3}{3a}\)

Xét hàm \(f\left(a\right)=\frac{\left(a-1\right)^3}{a}\Rightarrow f'\left(a\right)=\frac{2a^3-3a^2+1}{a^2}=\frac{\left(2a+1\right)\left(a-1\right)^2}{a^2}\) (\(a< 0\))

\(f\left(a\right)\) đạt cực tiểu tại \(a=-\frac{1}{2}\Rightarrow V_{min}=V\left(\frac{1}{2}\right)=\frac{9\pi}{4}\)