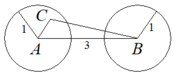
Cho 99 điểm trên mặt phăng trong đó có 2 điểm A và B cách nhau 3 cm. Mỗi nhóm 3 điểm bất kì của các điểm bất kì đã cho bao giờ cũng có thể chọn ra 2 điểm có khoản cách nhỏ hơn 1cm. Vẽ đường tròn (A ; 1cm) và (B ; 1 cm). Chứng tỏ rằng trong hai đường tròn chứa ít nhất là 50 điểm trong số các điểm đã cho.
Mk cần trả lời gấp!!!