Cho tam giác ABC cân tại A. Trên BC lấy M bất kỳ sao cho BM <CM. Từ M vẽ đường thẳng song song với AC cắt AB tại E và song song với AB cắt AC tại F. Gọi N là điểm đối xứng của M qua EF.
a) Tính chu vi tứ giác AEMF. Biết : AB =7cm
b) Chứng minh : AFEN là hình thang cân
c) Tính : ANB + ACB = ?
d) M ở vị trí nào để tứ giác AEMF là hình thoi và cần thêm điều kiện của ABC
để cho AEMF là hình vuông
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

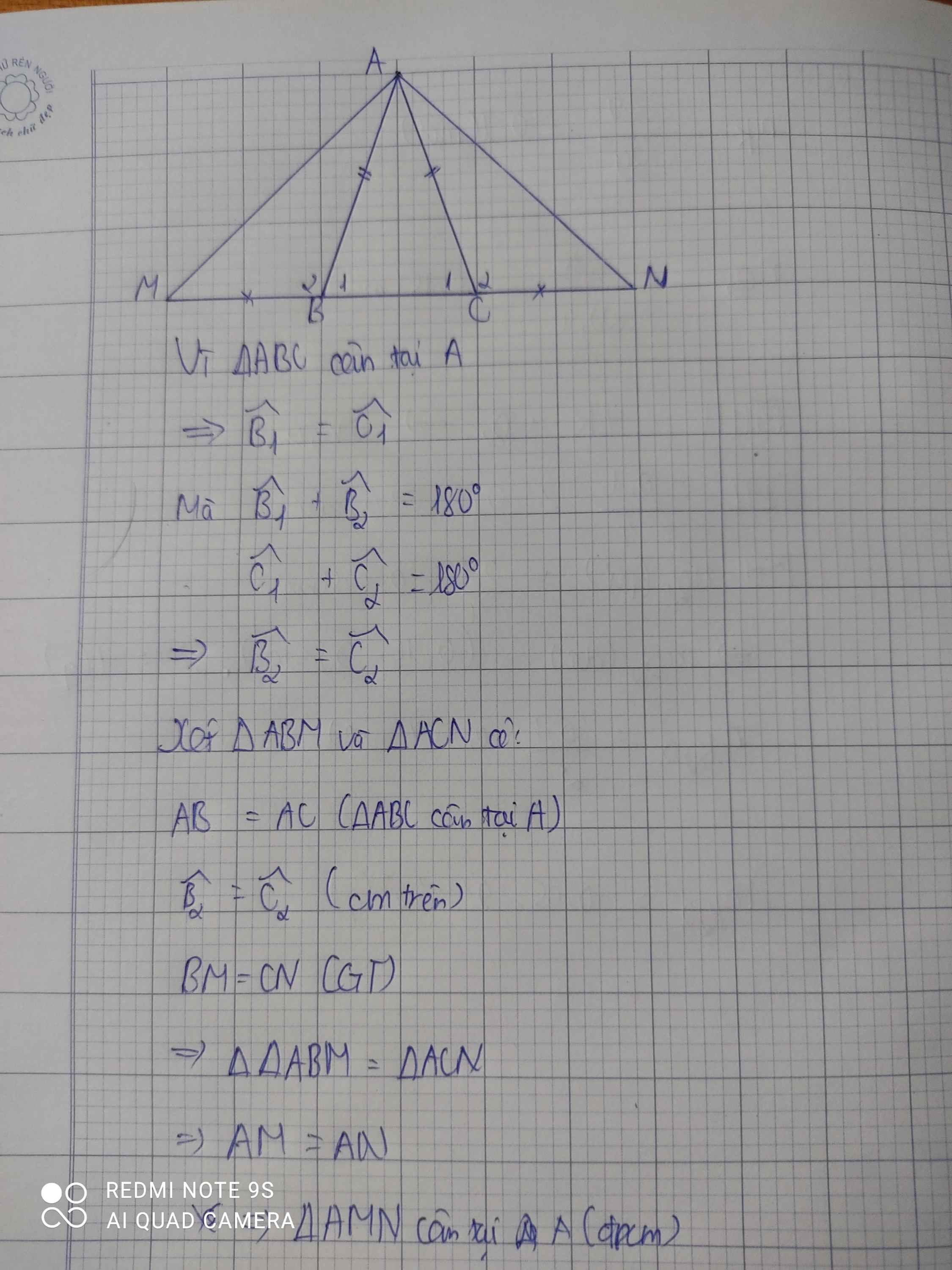
Vì tam giác ABC cân tại A
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\text{^}B_1=\text{^}C_1\end{matrix}\right.\)
Xét tam giác ABM và tam giác ACN có:
\(AB=AC\)(gt)
\(\text{^}B_2=\text{^}C_2\left(Vì\text{^}B_1=\text{^}C_1\right)\)
\(BM=CM\left(gt\right)\)
⇒ Tam giác ABM= tam giác ACN (c.g.c)
⇒ \(AM=AN\) (t/ứ)
⇒ Tam giác AMN cân tại A (đpcm)

Diện tích ABC: SABC = \(\frac{1}{2}2598\sqrt{2165^2-\frac{2598^2}{4}}\)
= 2249868 cm2
Gọi h1, h2 lần lượt là khoảng cách từ M đến AB, BC
ABxh1 + BCxh2 = SABC
=> 2165h1 + 2165h2 = 2249868
<=> 2165(h1 + h2) = 2249868
<=> h1 + h2 = \(\frac{2249868}{2165}\)= 1039.2

a: Ta có: ΔABC cân tại A
nên AB=AC
b: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
c: Ta có: ΔABM=ΔACN
nên AM=AN
hay ΔAMN cân tại A
 Bn tham khảo nhé!
Bn tham khảo nhé!