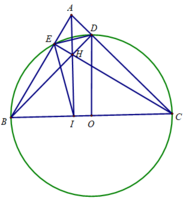
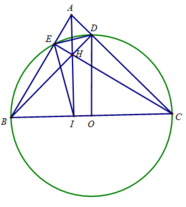
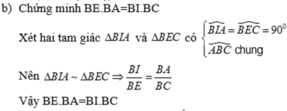Cho tam giác ABC nhọn . Đường tròn (O) đường kính BC cắt AB,AC lần lượt tại E và D.BD cắt CE tại H; AH cắt BC tại I.Vẽ cá tiếp tuyến AM và AN của (O) <M,N là các tiếp điểm >.CMR: M.H,N thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 1 2019
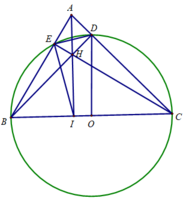
d) Tính BE.BA + CD.CA
Chứng minh tương tự câu b, CD.CA = CI.CB
Từ đó BE.BA + CD.CA = BI.BC + CI.CB
= (BI + CI).BC = BC.BC = B C 2 = 16 2 = 256
CM
17 tháng 2 2018
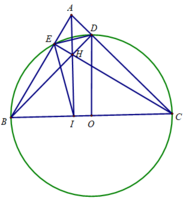
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)
10 tháng 5 2023
a: góc BEC=góc BDC=1/2*180=90 độ
=>CE vuông góc AB, BD vuông góc AC
góc AEH+góc ADH=180 độ
=>AEHD nội tiếp
b: góc EFH=góc ABD
góc DFH=góc ACE
mà góc ABD=góc ACE
nên góc EFH=góc DFH
=>FH là phân giác của góc EFD
30 tháng 4 2023
a: góc BEH+góc BKH=180 độ
=>BEHK nội tiếp
=>góc EBH=góc EKH
góc BKA=góc BDA=90 độ
=>ABKD nội tiếp
=>góc EBH=góc AKD=góc EKH
=>KA là phân giác của góc EKD
b: góc AIO=góc AJO=góc AKO=90 độ
=>I,J,K,A,O cùng thuộc đường tròn đường kính OA
sđ cung AI=sđ cung AJ
=>góc AKI=góc AJI
=>góc AKE+góc IKE=góc AKD+góc DKJ
=>góc IKE=góc DKJ
c:
