Cho ΔABC vuông tại A, AH ⊥ BC tại H. Trên cạnh BC lấy D sao cho BD = BA. Đường vuông góc với BC tại D cắt AC ở E
a) So sánh AE và DE
b) Chứng minh tia AD là tia phân giác của góc HAC
c) Vẽ DK vuông góc với AC tại K. Chứng minh rằng AK = AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó:ΔBAE=ΔBDE
Suy ra: EA=ED
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là phân giác của góc HAC

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
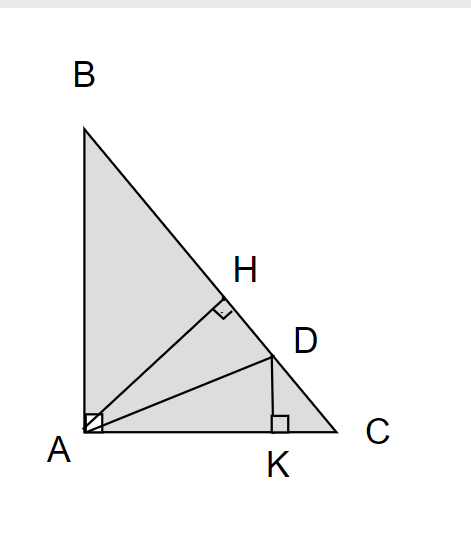
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)

a) Có góc DBH = góc AHB ( cùng = 90 º do cùng vuông góc BC ) mà 2 góc này ở vị trí so le trong nên BD song song AH.
Lại có BD = AH ( gt ) nên AHBD là hbh , vậy AB song song DH ( theo tính chất hbh )
b) Xét tam giác ABH có góc BAH = 35 º ( gt ) , góc AHB = 90 º do AH vuông góc BC.
Vậy góc ABC = 180º-90º-35º = 55º .
Do đó góc ACB = 180º - góc ABC - góc BAC
= 180º-90º-55º = 35º
a, vì BD=BA nên t.giác DBA caab tại B
=>\(\widehat{BDA}\)=\(\widehat{BAD}\)mà \(\widehat{EDB}\)=\(\widehat{A}\)=90 độ nên suy ra góc \(\widehat{EAD}\)=\(\widehat{EDA}\)
=>t.giác EAD cân tại E
=>AE=DE đpcm
b,vì ED và AH cùng vuông góc vs BC nên ED//AH
=> \(\widehat{EDA}\)=\(\widehat{DAH}\)(so le) mà \(\widehat{EDA}\)=\(\widehat{EAD}\)(t.giác AED cân tại E)
=>\(\widehat{DAH}\)=\(\widehat{EAD}\)
=> AD là p/g của góc HAC
c, xét 2 t.giác vuông AKD và AHD có:
AD chung
\(\widehat{KAD}\)=\(\widehat{HAD}\)(AD là p/g của \(\widehat{HAC}\))
=>t.giác AKD=t.giác AHD(CH-GN)
=>AK=AH
#HỌC TỐT#