Question

[Bùi Đức Toản]

Cho O là trung điểm của đoạn AB. Trên cùng một nửa mặt phẳng có bờ là cạnh AB vẽ tia Ax, By cùng vuông góc với AB. Trên tia Ax lấy điểm  C (khác A), qua O kẻ đường thẳng vuông góc với OC cắt tia By tại D.

a) Chứng minh AB²=4.AC.BD

b) Kẻ OM vuông góc với CD tại M. Chứng minh AC=CM

c) Từ M kẻ MH vuông góc AB tại H. Chứng minh BC đi qua trung điểm MH

d) Tìm vị trí của C trên tia Ax để diện tích tứ giác ABDC nhỏ nhất

Answer 1

[Thanh Tùng DZ]

Answer 2

[Thanh Tùng DZ]

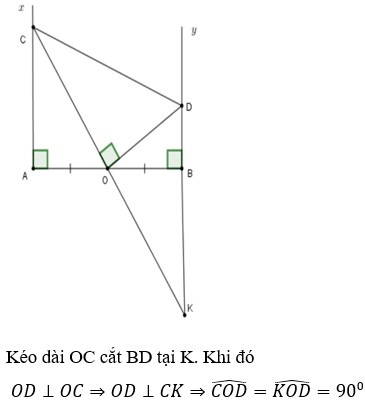
Xét \(\Delta OAC\)và \(\Delta DBO\)có :

\(\widehat{CAO}=\widehat{DBO}\left(=90^o\right)\); \(\widehat{COA}=\widehat{ODB}\)( cùng phụ \(\widehat{DOB}\))

\(\Rightarrow\)\(\Delta OAC\)~ \(\Delta DBO\)( g . g )

\(\Rightarrow\)\(\frac{OA}{BD}=\frac{AC}{BO}\) \(\Rightarrow\)OA . OB = BD . AC \(\Rightarrow\)AB² = 4BD . AC

b) \(\Delta OAC\)~ \(\Delta DBO\)(g.g) \(\Rightarrow\)\(\frac{AC}{AO}=\frac{OC}{OD}\)

xét \(\Delta OAC\)và \(\Delta DOC\)có : \(\frac{AC}{AO}=\frac{OC}{OD}\); \(\widehat{CAO}=\widehat{COD}=90^o\)

\(\Rightarrow\)\(\Delta OAC\)~ \(\Delta DOC\)(c.g.c) \(\Rightarrow\)\(\widehat{ACO}=\widehat{OCD}\)

xét \(\Delta OAC\)và \(\Delta MCO\)có : \(\widehat{ACO}=\widehat{OCD}\); CO ( chung )

\(\Rightarrow\)\(\Delta ACO=\Delta MCO\left(ch-gn\right)\)\(\Rightarrow\)CA = CM ; OA = OM ; 

c) OC là đường trung trực AM \(\Rightarrow\)OC \(\perp\)AM

Mặt khác : OA = OB = OM \(\Rightarrow\)\(\Delta AMB\)vuông tại M

\(\Rightarrow\)OC // BM

gọi gđ BM với AC là I

\(\Delta ABI\)có OC đi qua trung điểm AB và OC // BI \(\Rightarrow\)IC = AC

gọi K là gđ BC với MH

MH // AI \(\Rightarrow\)\(\frac{MK}{IC}=\frac{BK}{BC}=\frac{KH}{AC}\) \(\Rightarrow\)BK = KH 

\(\Rightarrow\)BC đi qua trung điểm MH

d) tứ giác ABDC là hình thang vuông \(\Rightarrow\)\(S_{ABDC}=\frac{1}{2}.\left(AC+BD\right).AB\)

Ta có : \(AC+BD\ge2\sqrt{AC.BD}=AB\)

\(\Rightarrow\)\(S_{ABDC}=\frac{1}{2}.\left(AC+BD\right).AB\ge\frac{1}{2}.AB^2\)

Dấu " = " xảy ra \(\Leftrightarrow\)AC = BD = \(\frac{AB}{2}=OA\)

Vậy C thuộc Ax và cách A 1 khoảng bằng OA