Cho các số thực x;y thỏa mãn (x-y)^2+(x^3-y^2)^2+6xy=36+(y^2-x^3)^2.Tìm giá trị lớn nhất A=xy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
21 tháng 12 2019
Đáp án C
Ta có
![]()

Khi đó

![]()
Vậy giá trị nhỏ nhất của biểu thức P là 3 + 2 2

CM
7 tháng 5 2018
Chọn C.
Phương pháp: Kiểm tra tính đúng sai của từng mệnh đề.
Cách giải:


AH
Akai Haruma
Giáo viên
18 tháng 8 2021
Bài 1:
$x-1=|2x-1|\geq 0\Rightarrow x\geq 1$
$\Rightarrow 2x-1>0\Rightarrow |2x-1|=2x-1$. Khi đó:
$2x-1=x-1\Leftrightarrow x=0$ (không thỏa mãn vì $x\geq 1$)
Vậy không tồn tại $x$ thỏa đề.
AH
Akai Haruma
Giáo viên
18 tháng 8 2021
Bài 2:
Nếu $x\geq \frac{1}{3}$ thì:
$3x-1=2x+3$
$\Leftrightarrow x=4$ (tm)
Nếu $x< \frac{1}{3}$ thì:
$1-3x=2x+3$
$\Leftrightarrow -2=5x\Leftrightarrow x=\frac{-2}{5}$ (tm)
Vậy......
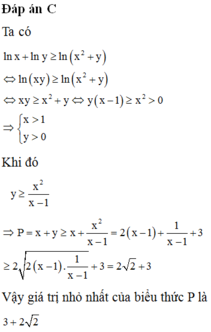

CÁC BẠN ƠI GIẢI NHANH MK VS ĐANG CẦN GẤP
cái này bạn áp dụng hằng đẳng thức đáng nhớ số 1
(x-y)^2+(x^3-y^2)^2+6xy=36+(y^2-x^3)^2
(x^2 + y^2 - 2xy) + (x^6 + y^4 - 2x^3*y^2) + 6xy = 36 + (y^4 + x^6 - 2x^3*y^2) (Vì nó bằng nên lược bớt)
x^2 + y^2 - 2xy + 6xy = 36
x^2 + y^2 + 4xy = 36
x^2 + y^2 + 2xy + 2xy = 36
(x + y)^2 + 2xy = 36