cho \(\widehat{AoB}=90^o\)tia Oc nằm giữa OA,OB . Tính \(\widehat{AoC}\)biết \(\frac{1}{4}AoC=\frac{1}{5}CoB\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
4 tháng 5 2019
a) tia Ob nằm giữa Oa và Ob vì :
^aOb+^bOc=^aOc
^aOb<^bOc(600<1200)
b) VìtiaObnằm giữa OavàOcnên:
^aOb+^bOc=^aOc
600+ ^bOc=1200
^bOc=1200−600
⇒ ^bOc=600
TiaOblàtiaphângiaccua^aOcvì:
^aOb+^bOc=^aOc
^aOb=^bOc=1600
P/s : bạn vào câu hỏi tương tự để xem thêm nhé !
F
6 tháng 7 2020
a,Vì ^AOB < ^AOC (60o < 120o)
=>OB nằm giữa OA và OC (1)
b,Ta có ^AOB + ^BOC = ^AOC
60o + ^BOC = 120o
^BOC = 60o
=>^AOB = ^BOC = 60o (2)
Từ (1) và (2)=>Ob là p/g ^AOC
c,TA có ^AOC + ^COD = 180o(góc bẹt)
=>^COD=180o - 120o
=>^COD=60o
=> ^COE=^EOD=\(\frac{60^o}{2}=30^o\)
Ta có: ^EOB=^BOC + ^COE
^EOB=60o + 30o
^EOB= 90o
T
10 tháng 3 2018
Ta có hình vẽ:
Đặt : Góc aOc = góc cOb
Ta có: \(\widehat{aOD}=\widehat{dOc}=\widehat{cOe}=\widehat{eOb}=\frac{1}{2}\widehat{aOc}=\frac{1}{2}\widehat{cOb}\)
\(\Rightarrow\widehat{aOc}=\widehat{cOb}=\frac{1}{2}+\frac{1}{2}=\frac{2}{2}=1\)
Vì đầu bài ta đã đặt: Góc aOc = góc cOb. Nên suy ra:
\(\widehat{dOe}=\widehat{aOc}=\widehat{cOb}=\frac{1}{2}+\frac{1}{2}=\frac{2}{2}=1\) (1)
Vì \(\widehat{aOb}=\widehat{aOc}+\widehat{cOb}=1+1=2\) (2)
Thế (1) và (2) vào ta có tỉ số của: \(\frac{\widehat{dOe}}{\widehat{aOb}}=\frac{1}{2}\)
CM
11 tháng 7 2018
Đáp án là B
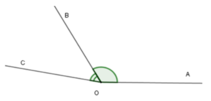
Vì tia OB nằm giữa hai tia OA và OC nên ∠AOB + ∠BOC = ∠AOC
Suy ra ∠AOC = 120 0 + 50 0 = 170 0
Hình bạn tự vẽ
Tia Oc nằm giữa 2 tia OA,OB nên
\(\widehat{AoC}\)\(+\)\(\widehat{CoB}\)\(=\)\(\widehat{AoB}\) \(\left(1\right)\)
=>\(\widehat{Aoc}+\widehat{CoB}\)\(=90^0\)
Theo đề ta có \(\frac{1}{4}AoC=\frac{1}{5}CoB\left(2\right)\)
Từ \(\left(2\right)\) \(\Rightarrow AoC=\frac{4}{5}CoB\)
Thay \(\frac{4}{5}CoB+CoB=90^0\)
\(=\frac{9}{5}CoB=90^0\)
\(CoB=90^0\div\frac{9}{5}=50^0\)