Xét tính đồng biến và nghịch biến của hàm số sau y = y= -x3 + 6x2 - 9x + 4
thách ai làm đc nếu làm đc thì
trong 3 ngày sẽ đc 3 tick nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

HẾT RỒI NHÉ ĐÁP ÁN LÀ :
+ Ta có: y '= 3x2 + 6x + m
+ Để hàm số đã cho đồng biến trên R thì y' ≥ 0,∀x ∈R
+ Yêu cầu bài toán trở thành tìm điều kiện của m để y' ≥ 0,∀x ∈R
Ta có y' = 3x2 + 6x + m, ta có: a = 3>0,Δ = 36 - 12m
Để y' ≥ 0,∀x ∈ R khi Δ ≤ 0 ⇔ 36 - 12m ≤ 0 ⇔ m ≥ 3
Vậy giá trị của tham số m cần tìm là m ≥ 3

a) TXĐ: R
y′ = 6x − 24 x 2 = 6x(1 − 4x)
y' = 0 ⇔ 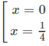
y' > 0 trên khoảng (0; 1/4) , suy ra y đồng biến trên khoảng (0; 1/4)
y' < 0 trên các khoảng ( - ∞ ; 0 ); (14; + ∞ ), suy ra y nghịch biến trên các khoảng ( - ∞ ;0 ); (14; + ∞ )
b) TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 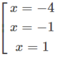
Bảng biến thiên:
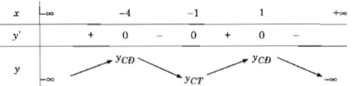
Vậy hàm số y đã cho đồng biến trên các khoảng ( - ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )
c) TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng ( - ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng ( - ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)
d) TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 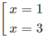
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng ( - ∞ ; 0) ⇒ y nghịch biến trên khoảng ( - ∞ ; 0)

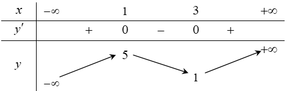
TXĐ: R
y′ = 3 x 2 − 12x + 9
y' = 0
y' > 0 trên các khoảng (- ∞ ; 1), (3; + ∞ ) nên y đồng biến trên các khoảng (- ∞ ; 1), (3; + ∞ )
y'< 0 trên khoảng (1; 3) nên y nghịch biến trên khoảng (1; 3)

Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.


Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.

Chọn D
Tập xác định: ![]() .
.
Đạo hàm: ![]() .
.
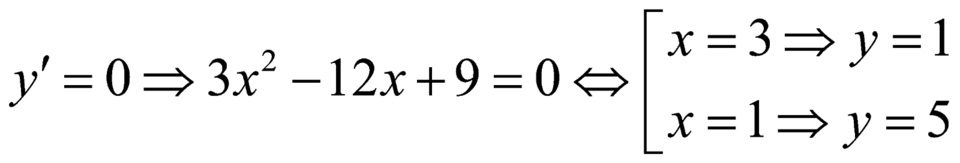 .
.
Bảng biến thiên:
Hàm số đồng biến trên các khoảng ![]() và
và ![]() .
.
Do đó hàm số nghịch biến trên khoảng ![]() .
.

TXĐ: R
y′ = 16 + 4x − 16 x 2 − 4 x 3 = −4(x + 4)( x 2 − 1)
y' = 0 ⇔ 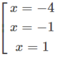
Bảng biến thiên:
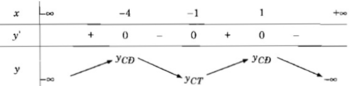
Vậy hàm số y đã cho đồng biến trên các khoảng (- ∞ ; -4) và (-1; 1), nghịch biến trên các khoảng (-4; -1) và (1; + ∞ )

Chọn đáp án D.
![]()
Do đó để phương trình f sin x = m có nghiệm trong khoảng (0;p)
thì phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ]
Quan sát đồ thị thấy phương trình f t = m có nghiệm t ∈ ( 0 ; 1 ] khi - 1 ≤ m < 1
đáp án là :
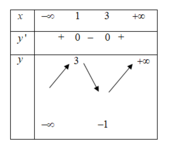
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔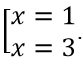
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
Hàm số đã cho xác định trên D=R.
Tính y' = -3x2 + 12x - 9. Cho y' = 0 ⇔ -3x2 + 12x - 9 = 0 ⇔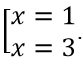
Bảng biến thiên:
Dựa vào bảng biến thiên,hàm số đồng biến trên (1;3).
Hàm số nghịch biến trên các khoảng (-∞; 1) và (3; +∞)
P/S : quá dễ , t là thần đồng mà .
Mỗi ngày 3 T i c k , giờ làm như lời hứa đi