Cho tam giác ABC.H là trực tâm,O là tâm đường tròn qua 3 đỉnh A,B,C.Chứng tỏ rằng khoảng cách từ O đến một cạnh bằng nửa khoảng cách từ H đến đỉnh đối diện.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
24 tháng 2 2020
O là tâm đường tròn ngoại tiếp tam giác ABC nên ta vẽ đường kính AOE
Tứ giác BHCE là hình bình hành
M là trung điểm của BC. Do đó M là trung điểm của HE.
Kết hợp với O là trung điểm của AE suy ra OM là đường trung bình của \(\Delta AHE\)
\(\Rightarrow OM=\frac{1}{2}AH\)hay 2OM = AH
Vậy khoảng cách từ trực tâm tới đỉnh bằng 2 lần khoảng cách từ giao điểm các đường trung trực tới cạnh đối diện đỉnh đó (đpcm)
CM
12 tháng 5 2019
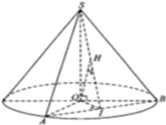
∆ O S A vuông cân OA = Ó = 1. ∆ S A B đều suy ra AB = 2 .
Kẻ O I ⊥ A B ⇒ O I = 1 2 A B = 2 2 .
Kẻ O H ⊥ S I ⇒ O H = d = 3 3
Đáp án B
CM
2 tháng 10 2018
Đáp án A
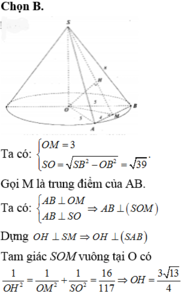
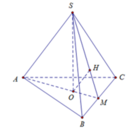
Ta có O M = 1 3 A M = a 3 3
Lại có d O ; S B C = O H = a 2 ⇒ S O = a
Mặt khác R N = O A = 2 a 3 3 ; h = S O = a ⇒ V = 1 3 π R 2 h = 4 π a 3 9
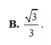
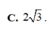
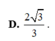
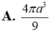
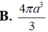
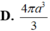
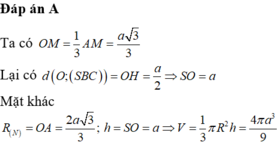
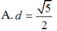
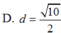
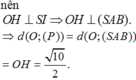
Câu hỏi của marivan2016 - Toán lớp 9 - Học toán với OnlineMath
Tham khảo nha!