Chứng minh rằng nếu tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k thì tỉ số của hai đường phân giác tương ứng của chúng cũng bằng k
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 10 2017
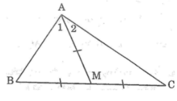
Vì AM là đường trung tuyến của ΔABC nên BM = MC = 1/2 BC
Mà AM = 1/2 BC (gt) nên: AM = BM = MC.
Tam giác AMB có AM = MB nên ΔAMB cân tại M
Suy ra: ∠B = ∠A1 (tính chất tam giác cân) (1)
Tam giác AMC có AM = MC nên ΔAMC cân tại M
Suy ra: ∠C = ∠A2 (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: ∠B + ∠C = ∠A1 + ∠A2 = ∠(BAC) (3)
Trong ΔABC ta có:
∠B + ∠C + ∠(BAC) = 180o (tổng ba góc trong tam giác) (4)
Từ (3) và (4) suy ra: ∠(BAC) + ∠(BAC) = 180o ⇔ 2∠(BAC) = 180o
Hay ∠(BAC) = 90o.
Vậy ΔABC vuông tại A.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 2 2021
\(\dfrac{b^2-a^2}{2c}=b.\dfrac{\left(b^2+c^2-a^2\right)}{2bc}-a.\dfrac{\left(a^2+c^2-b^2\right)}{2ac}\)
\(\Leftrightarrow\dfrac{b^2-a^2}{2c}=\dfrac{b^2+c^2-a^2}{2c}-\dfrac{a^2+c^2-b^2}{2c}\)
\(\Leftrightarrow b^2-a^2=\left(b^2+c^2-a^2\right)-\left(a^2+c^2-b^2\right)\)
\(\Leftrightarrow3b^2=3a^2\Leftrightarrow a=b\)
Hay tam giác cân tại C
GT
3
12 tháng 12 2017
vì \(\Delta ABC\)= \(\Delta NPM\)
\(\Rightarrow\)MN = NP ( 2 cạnh tương ứng ) ( 1 )
NP = PM ( 2 cạnh tương ứng ) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\)MN = NP = PM
Vậy tam giác MNP là tam giác đều
12 tháng 12 2017
Giải theo ý của mình nhé :
t/g MNP = t/g NPM ( giả thiết )
=> góc M = góc N
góc N = góc P
góc P = góc M
=> góc M = góc N = góc P
Nên t/g MNP là t/g đều
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
16 tháng 10 2015
Từ B kẻ đường cao BH (H thuộc AC)
\(S_{ABC}=\frac{1}{2}AC.BH\) (1)
Xét tam giác vuông ABH có
\(sinA=\frac{BH}{AB}\Rightarrow BH=AB.sinA\) (2)
Thay (2) vào (1) => \(S_{ABC}=\frac{1}{2}AB.AC.sinA\)
TV
1
HT
21 tháng 11 2016
Theo giả thiết ta có :
\(\Delta MNP=\Delta NPM\)
Suy ra:
- Góc M = góc N
- Góc N = góc P
- Góc P = góc N
\(\Rightarrow\)Góc M = góc N = góc P
Do vậy nên ta chứng minh được \(\Delta MNP\)là tam giác đều .
__tích_nha_bạn_chúc_bạn_học_giỏi__
Gọi AD và A'D' lần lượt là phân giác của tam giác ABC tại góc BAC và tam giác A'B'C' tại góc B'A'C'
tam giác ABC ~ tam giác A'B'C' => góc BAC = góc B'A'C'
=> góc BAD = 1/2 góc BAC = 1/2 góc B'A'C' = góc B'A'D' (AD và A'D' là phân giác)
Xét tam giác ABD và tam giác A'B'D' có :
1. góc ABD = góc A'B'D' ( do tam giác ABC ~ tam giác A'B'C' )
2. góc BAD = góc B'A'D' ( cmt )
Vậy tam giác ABD ~ tam giác A'B'D' (g-g)
=> AD/A'D' = AB/A'B' = k
CMTT cho phân giác 2 góc còn lại ta cũng có điều cần chứng minh.