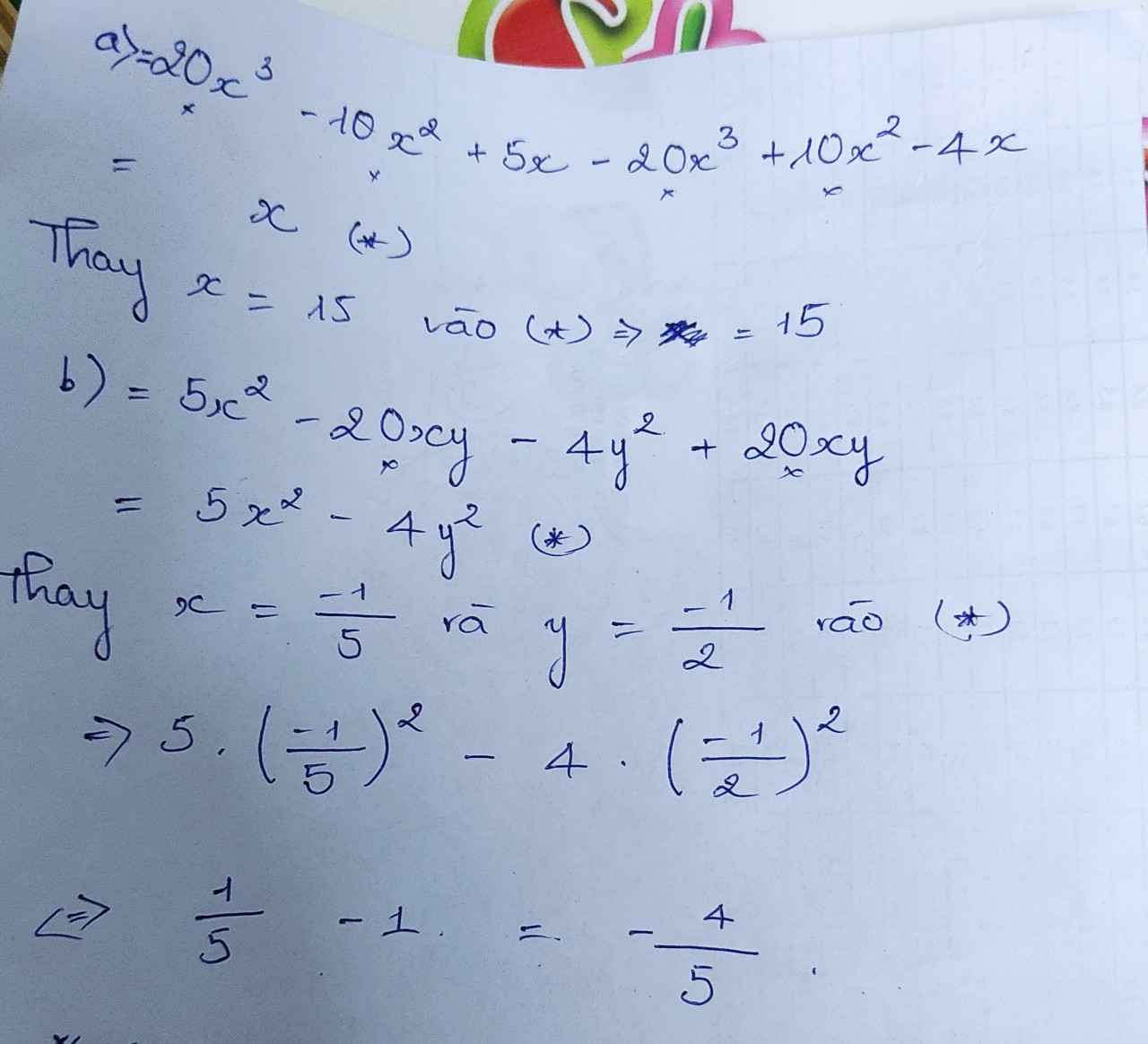Tìm \(x,y\ge0\) sao cho \(\left(x^2+4y+8\right)\left(y^2+4x+8\right)=\left(3x+5y+4\right)\left(5x+3y+4\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2019
\(VT=\left[\left(x-2\right)^2+4\left(x+y+1\right)\right]\left[\left(y-2\right)^2+4\left(x+y+1\right)\right]\)
\(VT=\left(x-2\right)^2\left(y-2\right)^2+4\left(x+y+1\right)\left[\left(x-2\right)^2+\left(y-2\right)^2\right]+16\left(x+y+1\right)^2\)
\(VP=\left[4\left(x+y+1\right)-\left(x-y\right)\right]\left[4\left(x+y+1\right)+\left(x-y\right)\right]\)
\(VP=16\left(x+y+1\right)^2-\left(x-y\right)^2\)
Ta có \(VT=VP\)
\(\Leftrightarrow\left(x-2\right)^2\left(y-2\right)^2+4\left(x+y+1\right)\left[\left(x-2\right)^2+\left(y-2\right)^2\right]=-\left(x-y\right)^2\)
\(\Leftrightarrow\left(x-2\right)^2\left(y-2\right)^2+4\left(x+y+1\right)\left[\left(x-2\right)^2+\left(y-2\right)^2\right]+\left(x-y\right)^2=0\) (1)
Nhận xét:
\(\left\{{}\begin{matrix}\left(x-y\right)^2\ge0\\\left(x-2\right)^2\left(y-2\right)^2\ge0\\x;y\ge0\Rightarrow4\left(x+y+1\right)>0\Rightarrow4\left(x+y+1\right)\left[\left(x-2\right)^2+\left(y-2\right)^2\right]\ge0\end{matrix}\right.\)
Vậy (1) xảy ra khi và chỉ khi:
\(\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(x-2\right)^2\left(y-2\right)^2=0\\\left(x-2\right)^2+\left(y-2\right)^2=0\end{matrix}\right.\) \(\Leftrightarrow x=y=2\)
Vậy phương trình đã cho có nghiệm duy nhất \(x=y=2\)
DP
12 tháng 7 2017
a) \(3x\left(x-2\right)-5x\left(1-x\right)-8\left(x^2-3\right)\)
\(=3x^2-6x-5x+5x^2-8x^2+24\)
\(=24-11x\)
b) \(\left(4x^2-3y\right)\cdot2y-\left(3x^2-4y\right)\cdot3y\)
\(=8x^2y-6y^2-9x^2y+12y^2\)
\(=6y^2-x^2y\)
c) \(3y^2\left[\left(2x-1\right)+y+1\right]-y\left(1-y-y^2\right)+y\)
\(=3y^2\cdot\left(2x-1+y+1\right)-y\cdot\left(1-y-y^2\right)+y\)
\(=6xy^2-3y^2+3y^3+3y^2-y+y^2+y^3+y\)
\(=4y^3+y^2+6xy^2\)
13 tháng 12 2022
a: \(\Leftrightarrow\left\{{}\begin{matrix}8x-4y+12-3x+6y-9=48\\9x-12y+9+16x-8y-36=48\end{matrix}\right.\)
=>5x+2y=48-12+9=45 và 25x-20y=48+36-9=48+27=75
=>x=7; y=5
b: \(\Leftrightarrow\left\{{}\begin{matrix}6x+6y-2x+3y=8\\-5x+5y-3x-2y=5\end{matrix}\right.\)
=>4x+9y=8 và -8x+3y=5
=>x=-1/4; y=1
c: \(\Leftrightarrow\left\{{}\begin{matrix}-4x-2+1,5=3y-6-6x\\11,5-12+4x=2y-5+x\end{matrix}\right.\)
=>-4x-0,5=-6x+3y-6 và 4x-0,5=x+2y-5
=>2x-3y=-5,5 và 3x-2y=-4,5
=>x=-1/2; y=3/2
e: \(\Leftrightarrow\left\{{}\begin{matrix}x\cdot2\sqrt{3}-y\sqrt{5}=2\sqrt{3}\cdot\sqrt{2}-\sqrt{5}\cdot\sqrt{3}\\3x-y=3\sqrt{2}-\sqrt{3}\end{matrix}\right.\)
=>\(x=\sqrt{2};y=\sqrt{3}\)
DH
12 tháng 7 2017
a, \(3x\left(x-2\right)-5x\left(1-x\right)-8\left(x^2-2\right)\)
\(=3x^2-6x-5x+5x^2-8x^2+16\)
\(=-11x+16\)
b, \(\left(4x^2-3y\right)2y-\left(3x^2-4y\right)3y\)
\(=8x^2y-6y^2-\left(9x^2y-12y^2\right)\)
\(=8x^2y-6y^2-9x^2y+12y^2=-x^2y+6y^2\)
c, \(3y^2\left[\left(2y-1\right)+y+1\right]-y\left(1-y-y^2\right)+y\)
\(=3y^2.3y-y+y^2+y^3+y\)
\(=9y^3+y^2+y^3=10y^3+y^2\)
Chúc bạn học tốt!!!
12 tháng 7 2017
a, \(3x\left(x-2\right)-5x\left(1-x\right)-8\left(x^2-2\right)\)
\(=3x^2-6x-5x+5x^2-8x^2+16\)
\(=-11x+16\)
b, \(\left(4x^2-3y\right)2y-\left(3x^2-4y\right)3y\)
\(=8x^2y-6y^2-9x^2y+12y^2\)
\(=-x^2y+6y^2\)
c, \(3y^2\left[\left(2y-1\right)+y+1\right]-y\left(1-y-y^2\right)+y\)
\(=3y^2.3y-y\left(1-y-y^2-1\right)\)
\(=9y^3-y\left(-y-y^2\right)\)
\(=9y^3+y^2+y^3=10y^3+y^2\)
31 tháng 5 2020
a)\(\left\{{}\begin{matrix}8x+2y=4\\8x+3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\4x+1=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}y=1\\x=\frac{1}{4}\end{matrix}\right.\)b)
\(\left\{{}\begin{matrix}12x-8y=44\\12x-15y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=35\\4x-5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\4x-5.5=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=5\\x=7\end{matrix}\right.\)c)\(\left\{{}\begin{matrix}9x=-18\\4x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\4.\left(-2\right)+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=7\end{matrix}\right.\)
