Cho tam giác ABC nhọn có AB = 15cm, BC = 14cm, AC = 13cm. Kẻ đường cao AH. Khi đó CH = ...
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.Xét tam giác ANH và tam giác AHC, có:
\(\widehat{ANH}=\widehat{AHC}=90^0\)
\(\widehat{NAH}=\widehat{HCA}\) ( cùng phụ với \(\widehat{A}\) )
Vậy tam giác ANH đồng dạng tam giác AHC ( g.g )
b. Xét tam giác AHB và tam giác ABC, có:
\(\widehat{BAC}=\widehat{AHB}=90^0\)
\(\widehat{B}:chung\)
Vậy tam giác AHB đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{BH}{AB}\)
\(\Leftrightarrow\dfrac{12}{13}=\dfrac{BH}{15}\)
\(\Leftrightarrow13BH=180\)
\(\Leftrightarrow BH=\dfrac{180}{13}cm\)
Xét tam giác AHC và tam giác ABC, có:
\(\widehat{CAB}=\widehat{CHA}=90^0\)
\(\widehat{C}:chung\)
Vậy tam giác AHC đồng dạng tam giác ABC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{CH}{AC}\)
\(\Leftrightarrow\dfrac{12}{15}=\dfrac{CH}{13}\) \(\Leftrightarrow\dfrac{4}{5}=\dfrac{CH}{13}\)
\(\Leftrightarrow5CH=52\)
\(\Leftrightarrow CH=\dfrac{52}{5}cm\)

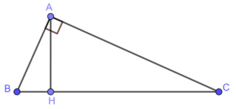
Ta có: A B 2 + A C 2 = 5 2 + 12 2 = 25 + 144 = 169 = 13 2 = B C 2
Suy ra, tam giác ABC vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
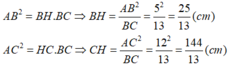

Bài 2:
Xét ΔABC có
\(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{144}{13}\left(cm\right)\end{matrix}\right.\)
Bài 1:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=900\)
\(\Leftrightarrow HC=36\left(cm\right)\)
hay HB=25(cm)

\(1,\dfrac{AB}{AC}=\dfrac{5}{6}\Leftrightarrow AB=\dfrac{5}{6}AC\)
Áp dụng HTL tam giác
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{900}=\dfrac{1}{\dfrac{25}{36}AC^2}+\dfrac{1}{AC^2}\\ \Leftrightarrow\dfrac{1}{900}=\dfrac{36}{25AC^2}+\dfrac{1}{AC^2}\\ \Leftrightarrow\dfrac{1}{900}=\dfrac{36+25}{25AC^2}\Leftrightarrow\dfrac{1}{900}=\dfrac{61}{25AC^2}\\ \Leftrightarrow25AC^2=54900\Leftrightarrow AC^2=2196\Leftrightarrow AC=6\sqrt{61}\left(cm\right)\\ \Leftrightarrow AB=\dfrac{5}{6}\cdot6\sqrt{61}=5\sqrt{61}\\ \Leftrightarrow BC=\sqrt{AB^2+AC^2}=61\left(cm\right)\)
Áp dụng HTL tam giác:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=...\\CH=\dfrac{AC^2}{BC}=...\end{matrix}\right.\)
Bài 1:
Ta có: \(\dfrac{AB}{AC}=\dfrac{5}{6}\)
\(\Leftrightarrow HB=\dfrac{25}{36}HC\)
Ta có: \(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{25}{36}=900\)
\(\Leftrightarrow HC=36\left(cm\right)\)
hay HB=25(cm)

Vẽ đường cao CH. Ta có:
\(\hept{\begin{cases}BH+AH=14\\BH^2+CH^2=225\\AH^2+CH^2=169\end{cases}\Rightarrow\hept{\begin{cases}BH+AH=14\\BH^2-AH^2=56\end{cases}\Leftrightarrow}\hept{\begin{cases}BH+AH=14\\\left(BH+AH\right)\left(BH-AH\right)=56\end{cases}\Leftrightarrow}\hept{\begin{cases}BH+AH=14\\BH-AH=4\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}BH=9\\AH=5\end{cases}\Rightarrow\hept{\begin{cases}\widehat{A}=cos^{-1}\frac{5}{13}\approx67^023'\\\widehat{B}=cos^{-1}\frac{9}{15}\approx53^08'\\\widehat{C}\approx180^0-\left(67^023'+53^08'\right)=59^029'\end{cases}}}\)

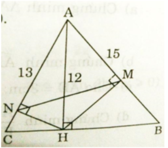
a) Xét ΔANH và ΔAHC có:
∠(NAH) chung
∠(ANH) = ∠(AHN) = 90o
⇒ ΔANH ∼ ΔAHC (g.g)
b) Ta có :
![]()
![]()
Tương tự : CH = 5 (cm)
⇒ BC = BH + CH = 9 + 5 = 14 (cm)
c) Theo chứng minh trên ta có:
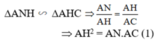
Chứng minh tương tự ta có :
ΔAMH ∼ ΔAHB ⇒ AH2 = AM.AB (2)
Từ (1) và (2) ⇒ AN.AC = AM.AB (3)
Xét ΔAMN và ΔACB có :
∠A chung
AN.AC = AM.AB
⇒ ΔAMN ∼ ΔACB (c.g.c)
d) Ta có : ΔAMH ∼ ΔAHB
![]()
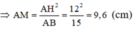
Lại có ΔAMN ∼ ΔACB (cmt)
![]()
![]()
\(cos\widehat{ACB}=\frac{AC^2+CB^2-AB^2}{2.AC.CB}=\frac{13^2+14^2-15^2}{2.13.14}=\frac{5}{13}\)
Xét ΔAHC vuông tại H
\(CH=cos\widehat{ACB}.AC=\frac{5}{13}.13=5cm\)
Cách khác:
Ta có:\(AB^2=AH^2+HB^2\)
Hay:\(AB^2=AC^2-HC^2+\left(BC-HC\right)^2\)
\(\Leftrightarrow225=169-HC^2+196-28HC+HC^2\)
\(\Leftrightarrow365-28HC=225\)
\(\Leftrightarrow28HC=140\)
\(\Leftrightarrow HC=5\)(cm)