Cho tam giác ABC, trên tia đối của AB lấy D sao cho AD=AB. Lấy G thuộc AC sao cho AG = 1/3.AC. Tia DG cắt BC tại E; qua E vẽ đường thẳng song song với BD; qua D vẽ đường thẳng song song với BC. Hai đường này cắt nhau tại F. Gọi M là giao của È và CD. Chứng minh 3 điểm B, G, M thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Tia DG cắt BC ở E.
21 tháng 5 2022
1: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
2: Xét ΔBCD có
BA là đường cao
BA là đường trung tuyến
Do đó: ΔBCD cân tại B
3: Xét ΔBCD có
BA là đường trung tuyến
CE là đường trung tuyến
BA cắt CE tại G
Do đó: G là trọng tâm của ΔBCD
=>AG=1/3BA=1(cm)
29 tháng 5 2022
Bạn tự vẽ hình nhé
a)
Áp dụng định lý Py-ta-go vào \(\Delta ABC:\)
\(BC^2=AB^2+AC^2\\ \Rightarrow BC^2=8^2+6^2\\ \Rightarrow BC^2=64+36\\ \Rightarrow BC^2=100\\ \Rightarrow BC=10\left(cm\right)\)
b)
Xét \(\Delta BGC\) và \(\Delta DGC\) có:
\(AB=AD\left(GT\right)\\ AG:chung\\ \widehat{BAC}=\widehat{DAC}\left(=90^o\right)\)
\(\Rightarrow\Delta BGC=\Delta DGC\left(c-g-c\right)\)
c)
Xét \(\Delta BCD\) có:
\(AB=AD\left(GT\right)\\ \dfrac{AG}{DG}=\dfrac{2}{6}=\dfrac{1}{3}\Rightarrow\dfrac{CG}{AC}=1-\dfrac{1}{3}=\dfrac{2}{3}\)
=> G là trọng tâm của \(\Delta BCD\)
=> DG là đường trung tuyến của \(\Delta BCD\) ứng với cạnh BC
Hay DG đi qua trung điểm BC
28 tháng 2 2022
a: Xét ΔABF và ΔADF có
AB=AD
\(\widehat{BAF}=\widehat{DAF}\)
AF chung
Do đó: ΔABF=ΔADF
b: Xét ΔABE và ΔADE có
AB=AD
\(\widehat{BAE}=\widehat{DAE}\)
AE chung
Do đó: ΔABE=ΔADE
Suy ra: EB=ED
c: Xét ΔBEG và ΔDEC có
BE=DE
\(\widehat{BEG}=\widehat{DEC}\)
EG=EC
Do đó: ΔBEG=ΔDEC
Suy ra: \(\widehat{EBG}=\widehat{EDC}\)
=>\(\widehat{EBG}+\widehat{ADE}=180^0\)
=>\(\widehat{EBG}+\widehat{EBA}=180^0\)
=>A,B,G thẳng hàng
Ta có:AB=AD
=>AC là đường trung tuyến
Mà AG=\(\frac{1}{3}\)AC nên:
=>G là trọng tâm
Ta có:tia DE cắt BC tại E nên:
=>DE là đường trung tuyến
=>BE=EC
Xét ΔDBE và ΔDEF có:
góc D1=góc D2 (so le trong) (DB//EF)
DE cạnh chung
góc FDG=góc E1 (so le trong)
=>ΔDBE=ΔDEF(g.c.g)
=>BE=DF(2 cạnh tương ứng)
Mà BE=EC nên EC=DF
Xét ΔDEM và ΔEMC có:
góc D3=góc C(so le trong) (DF//BE)
góc F=góc E3(so le trong) (DF//BE)
EC=DF (cmt)
=>ΔDEM=ΔEMC (g.c.g)
=>DM=MC (2 cạnh tương ứng)
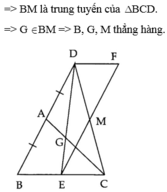
=>BM là đường trung tuyến
=>B,G,M thẳng hàng
CHÚC BN HC TỐT!!!^^