Trên cùng một nửa mặt phẳng bờ chứa tia Sa ,vẽ các tia Sb và Sc sao cho aSb=33 độ và aSc=66 độ.TẠi sao có thể khẳng định Sb là tia phân giác của góc aSc?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
12 tháng 7 2017
Đáp án C
Đặt SA=a.
![]()
=> tam giác ABC vuông tại B.
Gọi O là trung điểm của AC, khi đó OA=OB=OC => S, O cùng thuộc trục của đường tròn ngoại tiếp tam giác ABC, suy ra S O ⊥ ( A B C ) Do đó OB là hình chiếu vuông góc của SB lên mặt phẳng (ABC) nên góc giữa SB và (ABC) là:
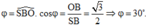
Trên cùng nửa mặt phẳng có bờ chứa tia Sa có \(\widehat{aSb}< \widehat{aS}c\left(33^0< 66^0\right).\)
\(\Rightarrow\)Sb là tia nằm giữa Sa và SC
còn tia phân giác thì k thể vì 66-33=30
Có tia Sb nằm giữa hai tia Sc và Sa vì góc aSb< góc aSc (33o< 66o)
\(\widehat{aSb}\)+\(\widehat{bSc}\)=\(\widehat{aSc}\)
33o+\(\widehat{bSc}\)=66o
\(\widehat{bSc}\)=66o-33o
Vậy \(\widehat{bSc}\)=33o
Nên aSb có thể khẳng định tia Sb là tia phân giác của aSb vì tia Sb nằm giữa hai tia Sb và Sc và aSb=bSc=33o