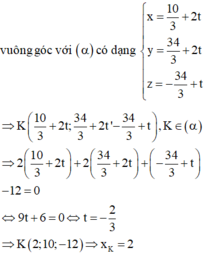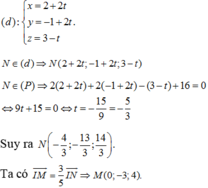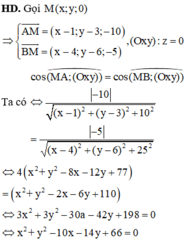Trên mặt phẳng tạo độ cho 2 điểm M(-3;2) và N (3;-2).Giải thích vì sao gốc tạo độ tại D và 2 điểm M và N là 3 điểm thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
4 tháng 2 2019
Đáp án B.
Gọi M x ; y ; z
⇒ A M → = x − 10 ; y − 6 ; z + 2 ; B M → = x − 5 ; y − 10 ; z + 9
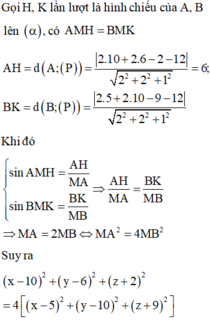
Gọi H, K lần lượt là hình chiếu của A, B lên
có A M H ^ = B M K ^ .
Khi đó sin A M H ^ = A H M A sin B M K ^ = B K M B
⇒ A H M A = B K M B ⇒ M A = 2 M B ⇔ M A 2 = 4 M B 2 .
Suy ra
x − 10 2 + y − 6 2 + z + 2 2 = 4 x − 5 2 + y − 10 2 + z + 9 2
⇔ x 2 + y 2 + z 2 − 20 3 x − 68 3 y + 68 3 z + 228 = 0 ⇔ S : x − 10 3 2 + y − 34 3 2 + z − 34 3 2 = R 2 .
Vậy M ∈ C là giao tuyến của α và S
→ Tâm I 2 ; 10 ; − 12 .
CM
6 tháng 3 2018
Đáp án B
Phương pháp:
+) Gọi M(x;y;z) tọa độ các véc tơ A M → , B M →
+) Gọi H, K lần lượt là hình chiếu của A,B lên ( α ) , có AMH = BMK
+) Tính sin các góc AMH = BMK và suy ra đẳng thức. Tìm quỹ tích điểm M là một đường tròn.
+) Tính tâm của đường tròn quỹ tích đó.
Cách giải:
Gọi M(x;y;z)
Gọi H, K lần lượt là hình chiếu của A, B lên ( α ) có AMH = BMK
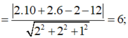
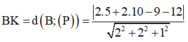
= 3
Khi đó
Suy ra
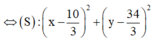
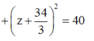
Vậy M ∈ (C) là giao tuyến của ( α ) và (S). Tâm K của (C) là hình chiếu của
I 10 3 ; 34 3 ; - 34 3 trên mặt phẳng ( α ) .
Phương trình đương thẳng đi qua I và vuông góc với ( α ) có dạng
27 tháng 1 2023
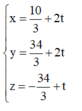
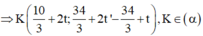
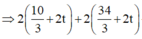
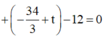
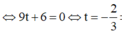
Trước hết ta đi tìm phương trình đường thẳng MN.
Gọi phương trình đường thẳng MN là \(MN:y=ax+b\).
Do \(M\in MN\) nên \(2=-3a+b\) \(\Leftrightarrow b=3a+2\) (1)
Mặt khác \(N\in MN\) nên \(-2=3a+b\) (2)
Từ (1) và (2) \(\Rightarrow-2=3a+3a+2\) \(\Leftrightarrow6a=-4\) \(\Leftrightarrow a=-\dfrac{2}{3}\)
Từ đó \(\Rightarrow b=3.\left(-\dfrac{2}{3}\right)+2=0\) . Vậy đường thẳng MN chính là đường thẳng \(y=-\dfrac{2}{3}x\) đi qua gốc tọa độ O. Từ đây suy ra M, O, N thẳng hàng.
15 tháng 2 2016
vì đồ thị của hàm số y = ax (a khác 0 ) là 1 đường thẳng đi qua góc tọa độ nên 3 điểm 0;m;n là 1 đường thẳng
