Cho phương trình \(x^2+6x+m=0.\)(với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt.Mọi người cho em hỏi em giải thế này có đúng chưa ạ? Nếu chưa thì mọi người giúp em với ạ! Em cảm ơn nhiều!Em giải thế này ạ:\(\Delta=36x^2-4x^2m.\)Để phương trình có 2 nghiệm phân biệtTương đương \(\Delta>0\)<=> \(36x^2-4x^2m>0\)<=>\(4x^2\left(9-m\right)>0\)<=>\(9-m>0\)<=>\(m<...
Đọc tiếp
Cho phương trình \(x^2+6x+m=0.\)
(với m là tham số). Tìm tất cả các giá trị của m để phương trình đã cho có 2 nghiệm phân biệt.
Mọi người cho em hỏi em giải thế này có đúng chưa ạ? Nếu chưa thì mọi người giúp em với ạ! Em cảm ơn nhiều!
Em giải thế này ạ:
\(\Delta=36x^2-4x^2m.\)
Để phương trình có 2 nghiệm phân biệt
Tương đương \(\Delta>0\)
<=> \(36x^2-4x^2m>0\)
<=>\(4x^2\left(9-m\right)>0\)
<=>\(9-m>0\)
<=>\(m< 8\)
Vậy m<8 để phương trình đã cho có 2 nghiệm phân biệt.
Thế này thì có đúng không ạ?
, 
, 
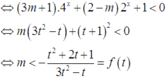
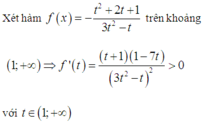
m<9 ạ em nhầm!
Mình nghĩ với pt tổng quát: \(ax^2+bx+c=0\) có \(\Delta=b^2-4ac\)
Nếu như vậy thì: \(1.x^2+6x+m\) có \(\Delta=6^2-4m\)chứ?
Riêng mình thì bài này mình dùng delta phẩy cho lẹ:
Lời giải
Để pt \(x^2+6x+m=0\) có 2 nghiệm phân biệt thì:
\(\Delta'=\left(\frac{b}{2}\right)^2-ac=3^2-m>0\)
\(\Leftrightarrow m< 9\)