Cho tam giác đều ABC có diện tích bằng 40 cm2. Ta vẽ tam giác vuông cân ACD có AC là cạnh huyền. Vẽ tiếp tam giác đều CDE. Tương tự như vậy vẽ tam giác vuông cân DEF và tam giác đều EFG. Hỏi tam giác đều EFG có diện tích bằng bao nhiêu?
help me >:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2019
Gọi M là trung điểm của BC, ta có:
AM = MB = 1/2 BC = a (tính chất tam giác vuông)
Suy ra MA = MB = AB = a
Suy ra ∆ AMB đều ⇒ ∠ (ABC) = 60 0
Mặt khác: ∠ (ABC) + ∠ (ACB) = 90 0 (tính chất tam giác vuông)
Suy ra: ∠ (ACB) = 90 0 - ∠ (ABC) = 90 0 – 60 0 = 30 0
Trong tam giác vuông ABC, theo Pi-ta-go, ta có: B C 2 = A B 2 + A C 2
⇒ A C 2 = B C 2 - A B 2 = 4 a 2 - a 2 = 3 a 2 ⇒ AC = a 3
Vậy S A B C = 1/2 .AB.AC
= 1 2 a . a 3 = a 2 3 2 ( đ v d t )
GD
3
I
18 tháng 3 2020
tam giác ABC đều => góc BAC =60 độ
tam giác ACD zuông cân ở C => góc CAD=45 độ
ta có góc BAD= góc BAC + góc CAD
=> góc BAD =60 độ +45 độ =105 độ
18 tháng 3 2020
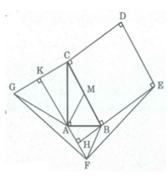
Ta có hình vẽ:
Ta có: \(\Delta ACD\) vuông cân tại C
\(\Rightarrow\widehat{CAD}=\widehat{CDA}=\frac{180^o-90^o}{2}=45^o\)
Lại có: \(\Delta ABC\)đều \(\Rightarrow\widehat{BAC}=\widehat{ABC}=\widehat{BCA}=60^o\)
\(\Rightarrow\widehat{BAD}=\widehat{BAC}+\widehat{CAD}\)
\(\Rightarrow\widehat{BAD}=60^o+45^o=105^o\)
Vậy \(\widehat{BAD}=105^o\)
HN
31 tháng 5 2017
a) Giả sử M là trung điểm của BC, \(\Delta ABM\) là tam giác đều nên \(\widehat{ABC}=60^o.\)
Từ đó suy ra: \(\widehat{BCA}=30^o\). Theo định lí Py-ta-go, ta có:
AC = \(\sqrt{BC^2-AB^2}\)
AC = \(\sqrt{4a^2-a^2}=a\sqrt{3}.\)
Do đó, ta có:
SABC = \(\dfrac{1}{2}AB.AC=\dfrac{1}{2}a^2\sqrt{3}.\) (1)
b) Vì \(\widehat{FAB}=\widehat{ABC}=60^o\) nên FA // BC (hai góc so le trong), từ đó suy ra FA vuông góc với BE và CG.
Gọi giao điểm của FA và BE là H, giao điểm của FA và CG là K. Ta có:
SFAG = \(\dfrac{1}{2}FA.GK=\dfrac{1}{2}a.\dfrac{a\sqrt{3}}{2}=\dfrac{1}{4}a^2\sqrt{3},\) (2)
SFBE = \(\dfrac{1}{2}BE.FH=\dfrac{1}{2}.2a.\dfrac{a}{2}=\dfrac{1}{2}a^2.\) (3)
c) SBDCE = 4a2, (4)
SABF = \(\dfrac{1}{4}a^2\sqrt{3},\) (5)
SACG = \(\dfrac{3}{4}a^2\sqrt{3}.\) (6)
Từ (1), (2), (3), (4), (5), (6), ta có:
SDEFG = \(\dfrac{a^2}{4}\left(18+7\sqrt{3}\right)\approx7,53a^2.\)
không cần làm nữa đâu ạ :)