Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và A'B', các tiếp tuyến chung CD và EF (A, A', C, E thuộc (O); B, B', D, F thuộc (O')). Gọi M là giao điểm của AB và EF, N là giao điểm của A'B' và CD, H là giao điểm của MN và OO'. Chứng minh rằng:
a) MN vuông góc với OO';
b) Năm điểm O', B, M, H, F thuộc cùng một đường tròn;
c) Năm điểm O, A, M, E, H thuộc cùng một đường tròn;
d) Ba điểm H, D, B thẳng hàng;
e) Ba điểm A, H, C thẳng hàng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

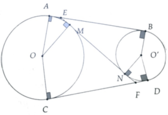
a, Ta có AB = AE + BE = EM + EN
Và CD = FD + FC = NF + NE
=> AB + CD = 2EF => AB = EF
b, Ta có EM = AB – EB = EF – EN = NF

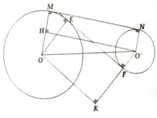
a, Kẻ O'H ⊥ OM; OK ⊥ O'F
có OH = R – r; O’K = R + r
Mà O H 2 = O O ' 2 - M N 2 = 36
O ' K 2 = O O ' 2 - E F 2 = 64
=> OH = 6 và O'K = 8
=> R = 7cm và r = 1cm
b, R = 17 2 cm và r = 7 2 cm

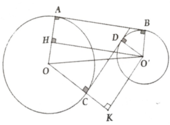
Kẻ O’H ⊥ OA; O’K ⊥ OC
OH = 4; OK = 8
Đặt CD = x => AB = 2x
O O ' 2 = 64 + x 2
và O O ' 2 = 16 + 4 x 2
=> x = 4 => OO' = 80 cm