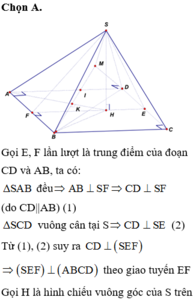
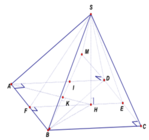
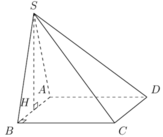
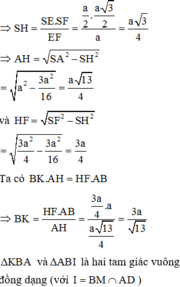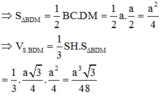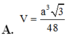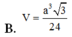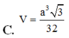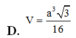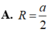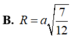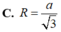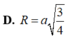Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và tam giác SCD vuông cân tại S. Gọi I, J lần lượt là trung điểm của AB, CD. Tính thể tích khối chóp S.AICJ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 6 2017
Đáp án D.
Phương pháp:
- Xác định chân đường cao của đỉnh S đến mặt phẳng đáy.
- Tính thể tích khối chóp: V = 1 3 S h
Cách giải:
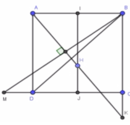
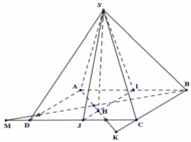
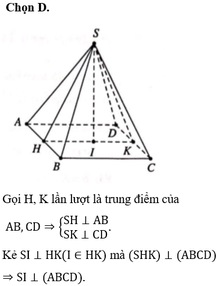
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB đều, tam giác SCD cân tại S nên S I ⊥ A B , S J ⊥ C D
Mà A B / / C D ⇒ A B , C D ⊥ S IJ
Dựng S H ⊥ I J , H ∈ I J ⇒ S H ⊥ A B C D (do S H ⊥ I J và S H ⊂ SIJ ⊥ C D )
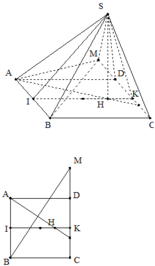
Trong (ABCD), kẻ
B M ⊥ A H , M ∈ C D , A H ∩ B M = T .
Khi đó, điểm M thỏa mãn điều kiện đề bài.
+) Δ S A B đều, cạnh a ⇒ S I = a 3 2
+) Δ S C D vuông cân tại S,
C D = a ⇒ S J = C D 2 = a 2
+) ABCD là hình vuông cạnh a
⇒ IJ = a
Tam giac SIJ có:
IJ 2 = S I 2 + S J 2 ⇒ Δ S I J vuông tại S.
Mà
S H ⊥ IJ ⇒ SI 2 = I H . IJ ⇒ a 3 2 2 = I H . a ⇒ I H = 3 a 4
Và
1 S H 2 = 1 S I 2 + 1 S J 2 = 1 a 3 2 2 + 1 a 2 2 = 16 3 a 2 ⇒ S H = a 3 4
Dễ dàng chứng minh Δ A I H đồng dạng tam giác
Δ B C M ⇒ S A I H S B M C = A I B C 2 = 1 4 ⇒ S B C M = 4 S A I H = 4. 1 2 . a 2 . 3 a 4 = 3 a 2 4
S B D M = S B C M − S B C D = 3 4 a 2 − 1 2 a 2 = a 2 4
Thể tích khối chóp S.BDM:
V S . B D M = 1 3 . S H . S B D M = 1 3 . a 3 4 . a 2 4 = 3 a 3 48
CM
23 tháng 10 2018
Đáp án D.
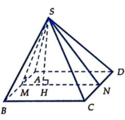
Gọi H là trung điểm của AB thì S H ⊥ A B C D ⇒ S H = a 2 .
Khoảng cách từ H đến BC, CD, DA đều là a 2 3 ⇒ S A B C D = 1 2 . a 2 3 . 9 a − a = 2 a 2 3 .
Vậy thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S H . S A B C D = 1 3 . a 2 . 2 a 2 3 = a 3 3 9 .
