Cho đường tròn (O) dây cung ST không phải đường kính, dựng điểm K đối xứng với S qua T. Điểm R tùy ý trên cung nhỏ ST sao cho đường tròn (RKT) cắt tiếp tuyến tại S của (O) tại 2 điểm phân biệt, gọi giao điểm gần S nhất là A. Đường thẳng AR cắt (O) ở L khác R. Chứng minh: KL là tiếp tuyến của (RKT) ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

22 tháng 2 2021
a) Xét (O) có
ΔBAC nội tiếp đường tròn(B,A,C\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔABC vuông tại C(Định lí)

CM
20 tháng 10 2019
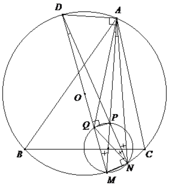
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.
Ta có: ^LST = ^LRT = ^AKT hay ^LST = ^SKA. Do SA là tiếp tuyến của (O) nên ^ASK = ^TLS
Xét \(\Delta\)SAK và \(\Delta\)LTS: ^LST = ^SKA, ^ASK = ^TLS => \(\Delta\)SAK ~ \(\Delta\)LST (g.g)
Suy ra: \(\frac{ST}{KA}=\frac{LS}{SK}\) hay \(\frac{SK}{2.KA}=\frac{LS}{2.TK}\) => \(\frac{SK}{KA}=\frac{LS}{TK}\)
Mà ^LSK = ^TKA (^LST = ^AKT) nên \(\Delta\)SLK ~ \(\Delta\)KTA (c.g.c) => ^LKS = ^TAK
Từ đó: ^TKL = ^TAK = 1/2.Sđ(TK(RKT) => KL tiếp xúc với (RKT) (đpcm).