tìm bộ ba số nguyên tố a,b,c có thể bằng nhau
abc<ab+bc+c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
1
AH
2 tháng 11 2018
a, Tổng của 3 số nguyên tố bằng 56 là một số chẵn
=> có 1 số nguyên tố là số chẵn
=> Số nhỏ nhất trong 3 số nguyên tố đó là : 2
b, Không vì 2017 là một số lẻ = số chẵn + số lẻ
+ Số chẵn lớn hơn 2 thì số đó chia hết cho 2 ( loại 0
+ Số chẵn bằng 2 thì số còn lại bằng 2015 chia hết cho 5 ( loại )
c) Goi số chia cho 12 dư 9 là a
=> a = 12k + 9 = 3 ( 4k + 3 ) chia hết cho 3
Do a chia hết cho 3
=> a không là số nguyên tố
d) Số p có 3 dạng : 3k,3k+1,3k+2
Nếu p = 3k thì p = 3 ( vì p là số nguyên tố ) , khi dó p + 2 = 5 và p + 4 = 7 là số nguyên tố
Nếu p = 3k + 1 thì p + 2 = 3k + 1 + 2 = 3k + 3 chia hết cho 3 và lớn hơn 3 nên p + 2 là hợp số (loại )
Nếu p = 3k + 2 thì p + 4 = 3k + 2 + 4 = 3k + 6 chia hết cho 3 và lớn hơn 3 nên p + 4 là hợp số ( loại )
Vậy p = 3 thỏa mãn yêu cầu đề bài
CT
22
DD
Đoàn Đức Hà
Giáo viên
8 tháng 3 2022
Ba số nguyên tố có tổng là \(38\)là một số chẵn nên trong ba số đó có số \(2\).
Tổng hai số còn lại là \(36\).
Gọi hai số đó là \(a,b\).
Ta có: \(a^2+b^2=\left(a+b\right)^2-2ab=36^2-2ab\)
Để \(\left(a^2+b^2\right)_{max}\)thì \(ab\)đạt min.
Nếu \(a=b\)thì \(a=b=18\)không là số nguyên tố.
Không mất tính tổng quát, giả sử \(a>b>0\)
Ta có nhận xét rằng \(a-b\)càng lớn thì \(ab\)càng nhỏ.
Thật vậy, nếu ta thay \(a\)bằng \(a+1\)và \(b\)bằng \(b-1\)thì:
\(\left(a+1\right)\left(b-1\right)=ab-a+b-1=ab-\left(a-b\right)-1< ab\).
Do đó để thỏa mãn ycbt thì ta cần tìm hai số nguyên tố \(a,b\)sao cho \(a+b=36\)và \(b\)nhỏ nhất.
Với \(b=3\Rightarrow a=33\)loại.
Với \(b=5\Rightarrow a=31\)(thỏa mãn)
Vậy ba số nguyên tố thỏa mãn ycbt là \(2,5,31\).
Khi đó tổng bình phương lớn nhất là: \(2^2+5^2+31^2=990\).
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 1 2022
a/ Nếu 2 số nguyên tố trên khác 2 thì 2 số đó phải là số lẻ => tổng chẵn
Mà tổng là 2001 lẻ => số thứ nhất phải là 2; số thứ 2 là 2001-2=1999
b/
Nếu 11 số nguyên tố đã cho đều khác 2 thì cả 11 số đều lẻ => tổng lẻ
Mà tổng của chúng theo đề bài là
2n là 1 số chẵn
=> số nguyên tố nhỏ nhất là 2
NH
1
8 tháng 7 2015
Gọi 3 số nguyên tố cần tìm là x,y,z ta có:
Cho x là số bằng 10% so với tổng 3 số cần tìm thì x=(x+y+z).10% = (x+y+z)/10
=> 10x= x+y+z
=> x+y+z là 1 số chẵn
=> 1 trong 3 số là số chẵn
=> Số nguyên tố chẵn duy nhất là 2, vậy 1 trong 3 số x,y,z là 2
10x = x+y+z nên 10x-x=y+z hay 9x=y+z
Vì y+z là số chẳn nếu y,z khác 2 nên x = 2
=> 18=y+z => {y;z}={5;13};{13;5};{7;11};{11;7}
=> y+z = 1 số chẵn + 1 số lẻ = 1 số lẻ.
=> Không tìm được x,y,z
MD
1
15 tháng 11 2015
Các bộ ba chữ số nguyên tố liên tiếp có thể là (2;3;5); (3;5;7)
Tính 22 + 32 + 52 = 4 + 9 + 25 = 38 là hợp số => Loại
Tính 32 + 52 + 72 = 9 + 25 + 49 = 83 là số nguyên tố
Vậy bộ ba số đó là 3;5; 7
PT
1
CM
24 tháng 9 2017
Vì a, b, c có vai trũ như nhau nên giả sử a ≤ b ≤ c khi đó
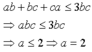
( Vì a là số nguyên tố )
Với a = 2 ta có
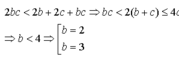
- Nếu b = 2 thì 4c < 2 + 4c thoả món với c là nguyên tố bất kỡ
- Nếu b = 3 thì 6c < 6b + 5c suy ra c < 6 vậy c = 3 hoặc c = 5
Vậy các cạp số (a, b, c) càn Tìm là (2, 2, p) ; (2, 3, 3 ) ; (2, 3, 5 ) và các hoán vị vủa chúng , với p là số nguyên tố .
TT
0
