Chỉ cần làm câu 18.19.20
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 4:
b) \(7x=4y\Rightarrow\dfrac{x}{4}=\dfrac{y}{7}\)
Áp dụng t/c dtsbn:
\(\dfrac{x}{4}=\dfrac{y}{7}=\dfrac{y-x}{4-7}=\dfrac{24}{-3}=-8\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).4=-12\\y=\left(-3\right).7=-28\end{matrix}\right.\)
c) Áp dụng t/c dtsbn:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{2x}{6}=\dfrac{3y}{12}=\dfrac{2x-3y}{6-12}=\dfrac{24}{-6}=-4\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-4\right).3=-12\\y=\left(-4\right).4=-16\end{matrix}\right.\)
Bài 3:
a: Ta có: \(\dfrac{2.5}{7.5}=\dfrac{x}{\dfrac{3}{5}}\)
\(\Leftrightarrow\dfrac{x}{\dfrac{3}{5}}=\dfrac{1}{3}\)
hay \(x=\dfrac{1}{5}\)
b: Ta có: \(\dfrac{5}{6}:x=\dfrac{20}{3}\)
\(\Leftrightarrow x=\dfrac{5}{6}:\dfrac{20}{3}=\dfrac{15}{120}=\dfrac{1}{8}\)

Bài 6:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{41}=\dfrac{b}{29}=\dfrac{c}{30}=\dfrac{a+b}{41+29}=\dfrac{700}{70}=10\)
Do đó: a=410; b=290; c=300

3.
\(D=2\left(x^2+4\right)+\left(y^2+1\right)+\dfrac{28}{x}+\dfrac{1}{y}-9\)
\(D\ge8x+2y+\dfrac{28}{x}+\dfrac{1}{y}-9\)
\(D\ge7\left(x+\dfrac{4}{x}\right)+\left(y+\dfrac{1}{y}\right)+x+y-9\)
\(D\ge14\sqrt{\dfrac{4x}{4}}+2\sqrt{\dfrac{y}{y}}+3-9=24\)
\(D_{min}=24\) khi \(\left(x;y\right)=\left(2;1\right)\)
Bài 4 và 6 trùng nhau?
\(A=\left(\dfrac{3x}{4}+\dfrac{3}{x}\right)+\left(\dfrac{y}{2}+\dfrac{9}{2y}\right)+\left(\dfrac{z}{4}+\dfrac{4}{z}\right)+\dfrac{1}{4}\left(x+2y+3z\right)\)
\(A\ge2\sqrt{\dfrac{9x}{4x}}+2\sqrt{\dfrac{9y}{4y}}+2\sqrt{\dfrac{4z}{4z}}+\dfrac{1}{4}.20\)
\(A\ge13\)
\(A_{min}=13\) khi \(\left(x;y;z\right)=\left(2;3;4\right)\)

a: \(B=\dfrac{16x-x^2-\left(2x+3\right)\left(x+2\right)+\left(3x-2\right)\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{\left(x+2\right)^2}{x-1}\)
\(=\dfrac{16x-x^2-2x^2-7x-6+3x^2-8x+4}{\left(x-2\right)}\cdot\dfrac{x+2}{x-1}\)
\(=\dfrac{x-2}{\left(x-2\right)}\cdot\dfrac{x+2}{x-1}=\dfrac{x+2}{x-1}\)
b: Để B=1/2 thì \(\dfrac{x+2}{x-1}=\dfrac{1}{2}\)
=>2x+4=x-1
=>x=-5

a/
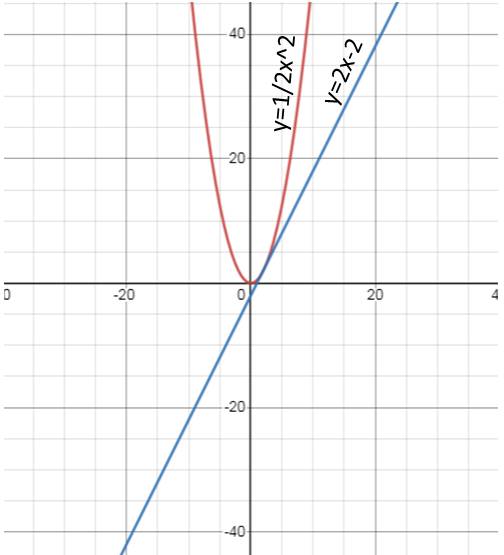
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)

a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AH=AK
=>ΔAKI=ΔAHI
=>KI=HI
AK=AH
IK=IH
=>AI là trung trực của HK


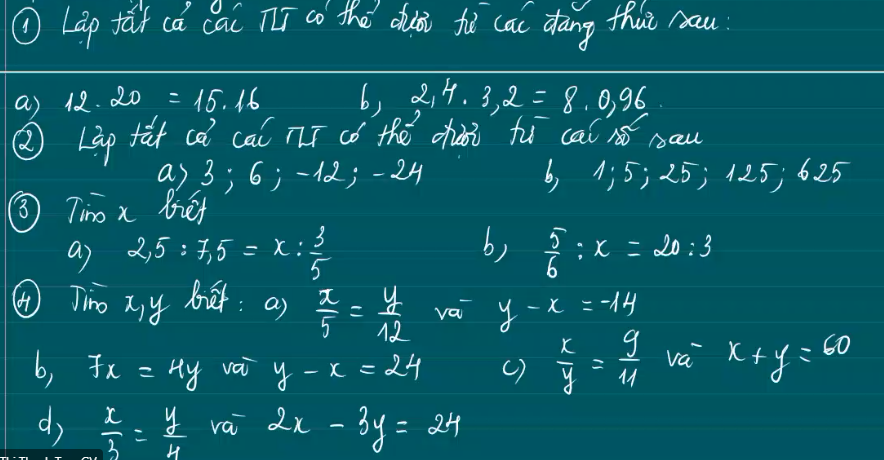

 mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17
mn ơi giúp em, nhanh ạ, chỉ cần làm đến bài 2 thôi,bài 1 chỉ cần làm đến câu 17 chỉ cần làm câu 3,4,5,6
chỉ cần làm câu 3,4,5,6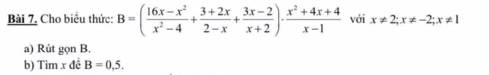
 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần

18. laughing
19. to do
20. doing
1. laughing
2. to do