cho tam giác ABC vuông tại A có AB=3 AC=4. tính độ dài véc tơ BC giúp mình với ạ:(
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng Pitago :
\(10^2=AB^2+AC^2\)
Ta có AB=3 và AC=4
=> 32+42=9+15=25=1/4(10^2)
=>AB=3 x 2 và AC =4x2
Thử :\(10^2=6^2+8^2\)
\(\Rightarrow100=36+84\)

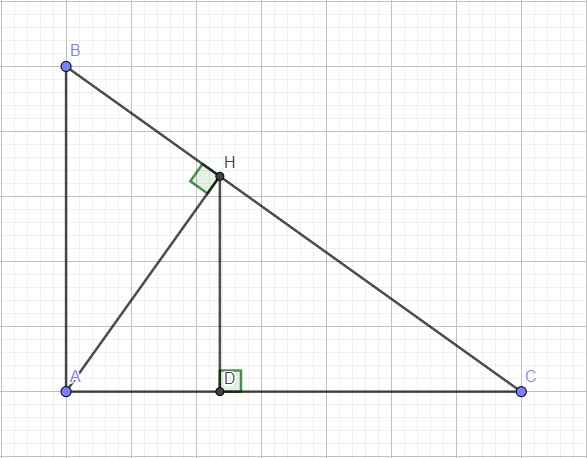
Áp dụng định lý Pitago cho tam giác vuông ACH:
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=\dfrac{25}{2}\) (cm)
\(\Rightarrow BH=BC-CH=\dfrac{9}{2}\left(cm\right)\)
Pitago tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}=\dfrac{15}{2}\left(cm\right)\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ACH:
\(HD.AC=AH.HC\Rightarrow HD=\dfrac{AH.HC}{AC}=\dfrac{24}{5}\left(cm\right)\)
Tiếp tục là hệ thức lượng:
\(AH^2=AD.AC\Rightarrow AD=\dfrac{AH^2}{AC}=\dfrac{18}{5}\left(cm\right)\)
\(S_{AHD}=\dfrac{1}{2}AD.HD=\dfrac{216}{25}\left(cm^2\right)\)

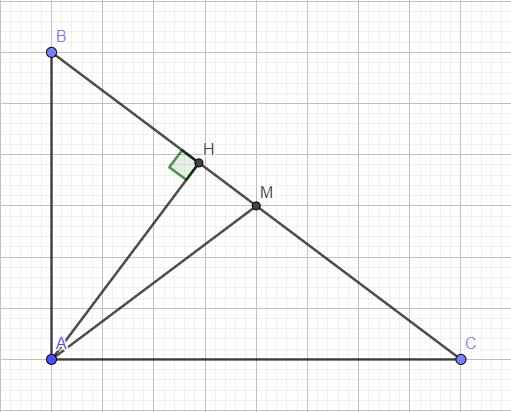
Áp dụng định lý Pitago:
\(BC=\sqrt{AB^2+AC^2}=5\)
Trong tam giác vuông ABC, AM là trung tuyến ứng với cạnh huyền
\(\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5}{2}\)
Áp dụng hệ thức lượng:
\(AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12}{5}\)
Áp dụng định lý Pitago cho tam giác vuông AHM:
\(HM=\sqrt{AM^2-AH^2}=\dfrac{7}{10}\)
\(\left|\overrightarrow{BC}\right|=BC=\sqrt{AB^2+AC^2}=5\)