giải phương trình nghiệm nguyên
a, 2xy +4y - x = 5
b, 2x + y = xy - 3
giúp mk vs nha. mk tik cho.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a,2xy+4y-x=5\\ \Leftrightarrow2y\left(x+2\right)-\left(x+2\right)=3\\ \Leftrightarrow\left(x+2\right)\left(2y-1\right)=3\\ Vìx,y\in Z\\ \Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2=1\\2y-1=3\end{matrix}\right.\\\left\{{}\begin{matrix}x+2=-1\\2y-1=-3\end{matrix}\right.\end{matrix}\right.và\left[{}\begin{matrix}\left\{{}\begin{matrix}x+2=3\\2y-1=1\end{matrix}\right.\\\left\{{}\begin{matrix}x+2=-3\\2y-1=-1\end{matrix}\right.\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\\\left\{{}\begin{matrix}x=-3\\y=-1\end{matrix}\right.\end{matrix}\right.và\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-5\\y=0\end{matrix}\right.\end{matrix}\right.\\ Vậy...........\)
\(b,2x+y=xy-3\\ \Leftrightarrow2x+y-xy+3=0\\ \Leftrightarrow x\left(2-y\right)-\left(2-y\right)+5=0\\ \Leftrightarrow\left(2-y\right)\left(x-1\right)=-5\\ \Leftrightarrow\left(y-2\right)\left(x-1\right)=5\\ Rồibntựxétnhé!!!!\)


a) Ta có: \(x^2-y^2-2x+2y\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-2\right)\)
b) Ta có: \(2x+2y-x^2-xy\)
\(=2\left(x+y\right)-x\left(x+y\right)\)
\(=\left(x+y\right)\left(2-x\right)\)
c) Ta có: \(x^2-25+y^2+2xy\)
\(=\left(x+y\right)^2-25\)
\(=\left(x+y-5\right)\left(x+y+5\right)\)
d) Ta có: \(3x^2-6xy+3y^2-12z^2\)
\(=3\left(x^2-2xy+y^2-4z^2\right)\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)
e) Ta có: \(x^2+2xy+y^2-xz-yz\)
\(=\left(x+y\right)^2-z\left(x+y\right)\)
\(=\left(x+y\right)\left(x+y-z\right)\)
f) Ta có: \(x^2-2x-4y^2-4y\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)

\(2x^2+y^2+2x-2xy+5-4y=0\)
\(\Leftrightarrow\left[y^2-2y\left(x+2\right)+\left(x+2\right)^2\right]+\left(x^2-2x+1\right)=0\)
\(\Leftrightarrow\left(y-x-2\right)^2+\left(x-1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y-x-2=0\\x-1=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=3\end{matrix}\right.\)
\(S=\left(x+2\right)^2+\left(y-1\right)^2=\left(1+2\right)^2+\left(3-1\right)^2\)
\(=3^2+2^2=13\)

a. 3x2 - 4y2 = 18
<=> \(\left\{{}\begin{matrix}3x^2=18+4y^2\\4y^2=-\left(3x^2-18\right)\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{18+4y^2}{3}}\\y=\sqrt{\dfrac{-3x^2+18}{4}}\end{matrix}\right.\)
b, c, d tương tự nhé
b. 19x2 + 28y2 = 2001
<=> \(\left\{{}\begin{matrix}19x^2=2001-28y^2\\28y^2=2001-19x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{\dfrac{2001-28y^2}{19}}\\y=\sqrt{\dfrac{2001-19x^2}{28}}\end{matrix}\right.\)
c. x2 = 2y2 - 8y + 3
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\8y=2y^2+3-x^2\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{2y^2-8y+3}\\y=\dfrac{2y^2+3-x^2}{8}\end{matrix}\right.\)
d. x2 + y2 - 4x + 4y = 1
<=> \(\left\{{}\begin{matrix}x^2=1-y^2+4x-4y\\y^2=1-x^2+4x-4y\end{matrix}\right.\)
<=> \(\left\{{}\begin{matrix}x=\sqrt{1-y^2+4x-4y}\\y=\sqrt{1-x^2+4x-4y}\end{matrix}\right.\)


d) \(x^2+y^2-4x+4y=1\\ \Rightarrow\left(x-2\right)^2+\left(y+2\right)^2=8\)
\(\Rightarrow8=\left(x-2\right)^2+\left(y+2\right)^2\ge\left(x-2\right)^2\)
\(\Rightarrow\left(x-2\right)^2\le8\)
Mà \(\left(x-2\right)^2\) là SCP và là số chẵn nên \(\left(x-2\right)^2\in\left\{0;4\right\}\)
Th1: \(\left(x-2\right)^2=0\Rightarrow\left(y+2\right)^2=8\left(vôlí\right)\)
Th2: \(\left(x-2\right)^2=4\Rightarrow\left(y+2\right)^2=4\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-2=-2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=-2\\y+2=2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=-2\end{matrix}\right.\\\left\{{}\begin{matrix}x-2=2\\y+2=2\end{matrix}\right.\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=0\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=0\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=-4\end{matrix}\right.\\\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left(x,y\right)\in\left\{\left(0;-4\right);\left(0;0\right);\left(4;-4\right);\left(4;0\right)\right\}\)

a, TK: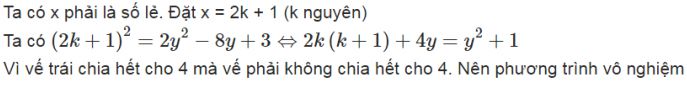
(x lẻ do \(2y^2-8y+3=2\left(y^2-4y\right)+3=x^2\) lẻ)
\(b,\Leftrightarrow\left(x^2-4x+4\right)+\left(y^2+4y+4\right)=9\\ \Leftrightarrow\left(x-2\right)^2+\left(y+2\right)^2=9\)
Vậy pt vô nghiệm do 9 ko phải tổng 2 số chính phương
\(a)2xy+4y-x=5\)
\(\Leftrightarrow\left(2xy+4y\right)-x=3+2\)
\(\Leftrightarrow2y\left(x+2\right)-x-2=3\)
\(\Leftrightarrow2y\left(x+2\right)-\left(x+2\right)=3\)
\(\Leftrightarrow\left(x+2\right)\left(2y-1\right)=3\)
\(\Rightarrow\left(x+2\right);\left(2y-1\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Xét từng trường hợp :
Vậy
\(2x+y=xy-3\)
\(\Leftrightarrow xy-2x-y=3\)
\(\Leftrightarrow\left(xy-2x\right)-y=-2+5\)
\(\Leftrightarrow x\left(y-2\right)-y+2=5\)
\(\Leftrightarrow x\left(y-2\right)-\left(y-2\right)=5\)
\(\Leftrightarrow\left(y-2\right)\left(x-1\right)=5\)
\(\Rightarrow\left(y-2\right);\left(x-1\right)\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Xét các trường hợp như câu trên và kết luận