Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Qua A kẻ một cát tuyến bất kỳ cắt (O) tại C và (O’) tại D. Chứng minh rằng OC // O’D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AH
Akai Haruma
Giáo viên
15 tháng 3 2021
Lời giải:
Gọi $H$ là giao điểm $MN$ và $OA$.
$AM=AN; OM=ON$ nên $OA$ là trung trực của $MN$. Do đó $OA\perp MN$ tại $H$
$\Rightarrow \widehat{AHQ}=90^0$
Tứ giác $AHDQ$ có $\widehat{AHQ}=\widehat{ADQ}=90^0$ và cùng nhìn cạnh $AQ$ nên $AHDQ$ nội tiếp
$\Rightarrow OD.OQ=OH.OA(1)$
Mà xét tam giác $AMO$ vuông tại $M$ có đường cao $MH$, thì theo hệ thức lượng trong tam giác vuông ta có: $R^2=OM^2=OH.OA(2)$
Từ $(1);(2)\Rightarrow OD.OQ=R^2$ (đpcm)
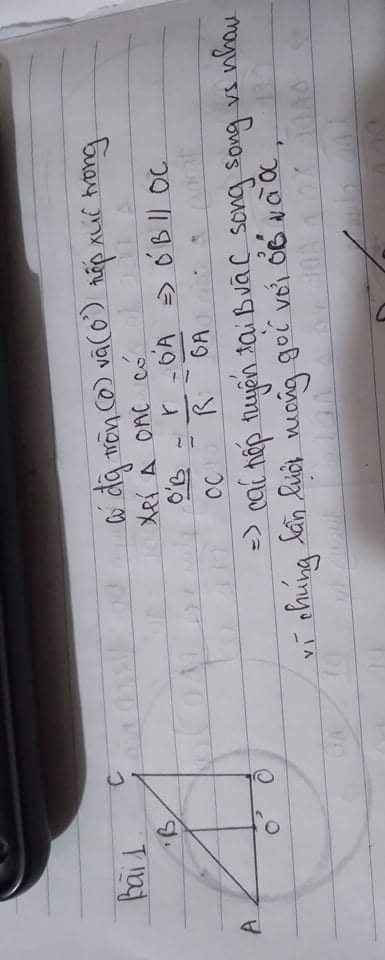
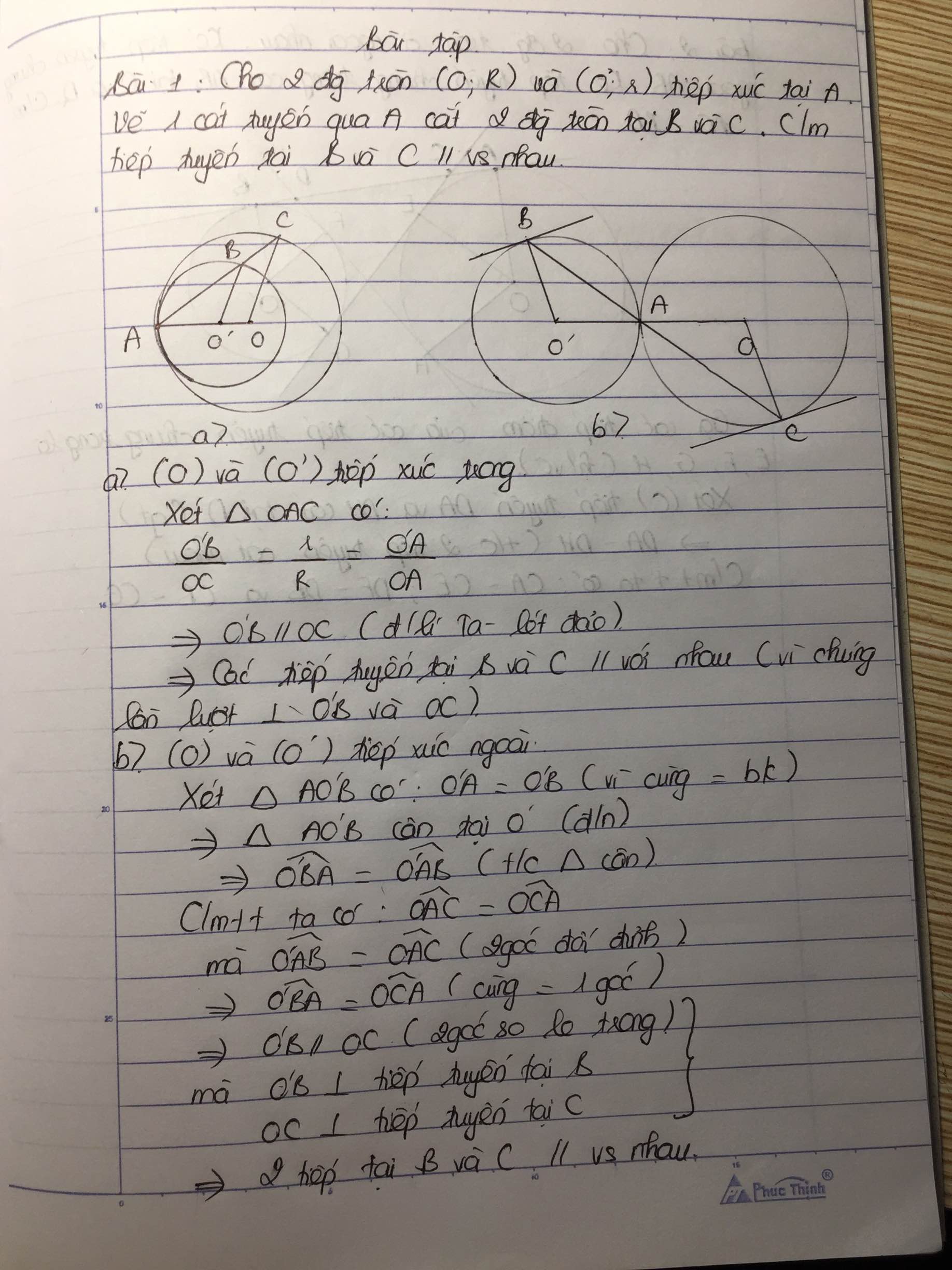

Ta có \(\widehat{OAC}=\widehat{O'AD}\left(đối.đỉnh\right)\)
Mặt khác \(\Delta OAC.cân.tại.O\left(OA=OC\right)\)
Nên \(\widehat{OAC}=\widehat{OCA}\)
Tương tự \(\Delta O'AD.cân.tại.O'\left(O'A=O'D\right)\)
Nên \(\widehat{O'AD}=\widehat{O'DA}\)
\(\Rightarrow\widehat{OCA}=\widehat{ADO'}\)
Mà 2 góc này ở vị trí so le trong
Vậy \(OC//O'D\)