K
Khách
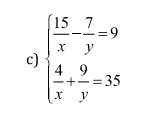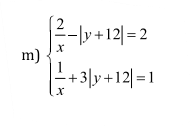
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BT
0
Những câu hỏi liên quan
4 tháng 10 2021
\(1,3x+2y=7\\ \Leftrightarrow2y=7-3x\left(1\right)\)
Vì \(2y⋮2\)
\(\Leftrightarrow3x-7⋮2\\ \Leftrightarrow3x-9⋮2\\ \Leftrightarrow3\left(x-3\right)⋮2\\ \Leftrightarrow x-3⋮2\\ \Leftrightarrow x.lẻ\)
Đặt \(x=2k+1\left(k\in Z\right)\)
Thay vào (1), ta được :
\(\left(1\right)\Leftrightarrow2y=3\left(2k+1\right)-7\\ \Leftrightarrow2y=6k+3-7\\ \Leftrightarrow2y=6k-4\\ \Leftrightarrow y=3k-2\)
Vậy \(x=2k+1;y=3k-2\left(k\in Z\right)\)
\(2,C_1:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+2y=2\\4x+5y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x+5y=2\\7y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{7}\\y=\dfrac{5}{7}\end{matrix}\right.\\ C_2:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1+2x\\4x+5y=3\end{matrix}\right.\Leftrightarrow4x+5+10x=3\\ \Leftrightarrow x=-\dfrac{1}{7}\Leftrightarrow y=1-\dfrac{2}{7}=\dfrac{5}{7}\)
3 tháng 1 2022
\(\Leftrightarrow\left\{{}\begin{matrix}-x+3y=1\\2\left(x-3y\right)=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)
23 tháng 10 2021
b: \(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=4\\4x+2y=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-6\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=5-2x=5-12=-7\end{matrix}\right.\)
D
1
22 tháng 12 2021
\(\left(2\right)\Leftrightarrow\left|x-1\right|=3-3y\)
Thay vào \(\left(1\right)\Leftrightarrow3-3y+\left|y-2\right|=1\Leftrightarrow\left|y-2\right|=3y-2\)
\(\Leftrightarrow\left[{}\begin{matrix}y-2=3y-2\left(y\ge2\right)\\2-y=3y-2\left(y< 2\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=0\left(tkm\right)\\y=1\left(tm\right)\end{matrix}\right.\)
Với \(y=1\Leftrightarrow\left|x-1\right|=3-3=0\Leftrightarrow x=1\)
Vậy \(\left(x;y\right)=\left(1;1\right)\)
7 tháng 3 2022
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{135}{x}-\dfrac{63}{y}=81\\\dfrac{28}{x}+\dfrac{63}{y}=245\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{163}{x}=326\\\dfrac{4}{x}+\dfrac{9}{y}=35\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\\dfrac{9}{y}=35-\dfrac{4}{x}=35-8=27\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=\dfrac{1}{3}\end{matrix}\right.\)
TN
8 tháng 3 2018
Gọi số thứ nhất là x
\(\Rightarrow\)Số thứ hai là 19-x
Theo đề bài ta có phương trình:
x2+(19-x)2=185
\(\Leftrightarrow x^2+361-38x+x^2=185\)
\(\Leftrightarrow2x^2-38x+361-185=0\)
\(\Leftrightarrow2x^2-38x+176=0\)
\(\Leftrightarrow x^2-19x+88=0\)
\(\Leftrightarrow x^2-11x-8x+88=0\)
\(\Leftrightarrow x\left(x-11\right)-8\left(x-11\right)=0\)
\(\Leftrightarrow\left(x-11\right)\left(x-8\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-11=0\\x-8=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=11\\x=8\end{cases}}\)
Vậy số thứ nhất là 8, số thứ hai là 19-8=11 hoặc số thứ nhất là 11, số thứ hai là 19-11=8
ML
3
18 tháng 10 2021
2x+y=-4
\(\Leftrightarrow2x=-4-y\)
\(\Leftrightarrow x=\dfrac{-y-4}{2}\)
Ta có: 3x+|y|=-1
\(\Leftrightarrow\dfrac{-3y-12}{2}+\left|y\right|=-1\)
\(\Leftrightarrow\left|y\right|=\dfrac{-2+3y+12}{2}=\dfrac{3y+10}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{3}{2}y+5\left(y\ge0\right)\\y=-\dfrac{3}{2}y+5\left(y< 0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{-1}{2}y=5\\\dfrac{5}{2}y=5\end{matrix}\right.\Leftrightarrow y\in\varnothing\)
17 tháng 6 2021
a) đk \(x\ge\dfrac{-3}{2}\)
PT <=> \(4x^2\left(2x+3\right)=\left(3x^2+6x+1\right)^2\)
<=> \(8x^3+12x^2=9x^4+36x^2+1+36x^3+12x+6x^2\)
<=> \(9x^4+28x^3+30x^2+12x+1=0\)
<=> \(\left(x+1\right)^3\left(9x+1\right)=0\)
<=> \(\left[{}\begin{matrix}x=-1\left(c\right)\\x=\dfrac{-1}{9}\left(l\right)\end{matrix}\right.\)
KL: PT có nghiệm duy nhất x = -1
b) đk: \(x\ge-1;x\ge2y\)
hpt <=> \(\left\{{}\begin{matrix}2x^2-4xy+3y-4x-4=\sqrt{9\left(x-1\right)\left(x+1\right)\left(x-2y\right)}\left(1\right)\\2x-2y+1+2\sqrt{\left(x+1\right)\left(x-2y\right)}=2x-2y+5\left(2\right)\end{matrix}\right.\)
(2) <=> \(\sqrt{\left(x+1\right)\left(x-2y\right)}=2\)
<=> \(\left(x+1\right)\left(x-2y\right)=4\)
(1) <=> 2(x+1)(x-2y) + x - 4 = \(6.\sqrt{x-1}\)
<=> x+4 = \(6\sqrt{x-1}\)
<=> x2 + 8x + 16 = 36x - 36
<=> x2 -28x + 52 = 0
<=> (x-26)(x-2) = 0
<=> \(\left[{}\begin{matrix}x=26< =>y=\dfrac{349}{27}\\x=2< =>y=\dfrac{1}{3}\end{matrix}\right.\)
