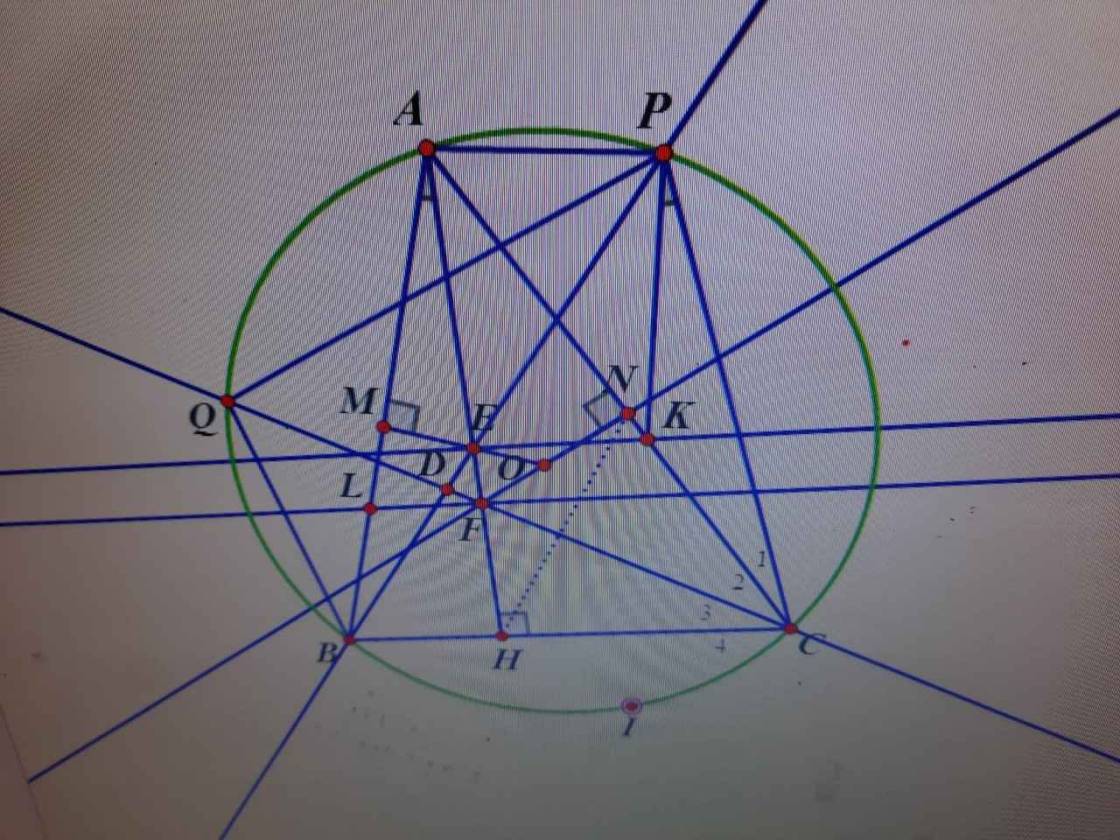
Cho tam giác ABC có 3 góc nhọn ,nội tiếp đường tròn tâm O. Các đường cao AD,BE,CF của tam giác ABC đồng quy tại H. P là điểm thuộc cung nhỏ AC của đường tròn tâm O. Gọi M,I lần lượt là trung điểm các đoạn thẳng BC và HP, Chứng minh \(MI\perp AP\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét tứ giác AEHF có
góc AEH+góc AFH=180 độ
=>AEHF là tứ giác nội tiếp
Xét tứ giác BFEC có
góc BFC=góc BEC=90 độ
=>BFEC là tứ giác nội tiếp
b: Xét (O) có
ΔABK nội tiếp
AK là đường kính
=>ΔABK vuông tại B
=>BK//CH
Xét (O) có
ΔACK nội tiếp
AK là đường kính
=>ΔACK vuông tại C
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>I là trung điểm của BC

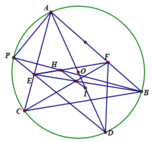
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.

bạn ơi cho mình hỏi bài này ở đề năm bao nhiêu của thành phố nào vậy bạn?????
3. Xét tứ giác BFHD có:
HFB + HDB = 90º + 90º = 180º => BFHD là tứ giác nội tiếp. ⇒ FBH = FDH (1)
Tương tự có DHEC là tứ giác nội tiếp, ⇒HCE = HDE (2)
Mà BFEC là tứ giác nội tiếp nên FCE = FBE (3)
Từ (1) (2) (3)⇒ 2ABE = FDH + HDE = FDE
Vì BFEC là tứ giác nội tiếp đường tròn tâm I, đường kính BC nên theo quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung EF, ta có: FIE = 2.FBE = 2.ABE
⇒FIE = FDE
4.Vì BFEC là tứ giác nội tiếp nên:
ABC = 180º – FEC = AEF => ΔAEF ~ ΔABC (g.g)![]()
Suy ra độ dài EF không đổi khi A chạy trên cung lớn BC của đường tròn (O)
Gọi K là giao điểm thứ 2 của ED và đường tròn đường kính BC
Theo tính chất góc ngoài: FDE = DKE + DEK
Theo ý 3 và quan hệ giữa góc ở tâm và góc nội tiếp cùng chắn cung, có FDE = FIE = 2.DKE
⇒DKE = DEK => ΔDEK cân tại D => DE = DK
Chu vi ΔDEF là P = DE + EF + FD = EF + FD + DK = EF + FK
Có FK ≤ BC ( dây cung – đường kính) => P ≤ EF + BC không đổi
Dâu bằng xảy ra khi và chỉ khi FK đi qua I ⇔ D trùng I ⇔ ΔABC cân tại A.
Vậy A là điểm chính giữa của cung lớn BC


a)
xét tứ giác AEHF có :
AEH = 900 (BE là đường cao của B trên AC )
AFH = 900 (CF là dường cao của C trên AB )
ta có ; AEH + AFH = 1800 mà 2 góc này ở vị trí đối nhau
==> tứ giác AEHF nội tiếp
xét tứ AEDB có :
AEB = 900 (BE là dường cao của B trên AC )
ADB = 900 (AD là đường cao của A trên BD )
mà 2 góc này cùa nhìn cạnh AB dưới một góc vuông
==> tứ giác AEDB nội tiếp
câu b vì mình ko hiểu đường cao của đường tròn là gì :/

a) Gọi BH cắt (O) tại S khác B. Qua tính chất quen thuộc của trực tâm ta thấy H,S đối xứng nhau qua AC.
Do đó ^ASE = ^AHE = 900 (Vì HE // BC, AH vuông góc BC) hay SE vuông góc với AS (1)
Ta có AD là đường kính của (O) => ^ASD chắn nửa (O) => SD vuông góc với AS (2)
Từ (1) và (2) suy ra SE trùng SD hay DE cắt (O) tại S. Như vậy BH,DE cắt nhau trên (O) (đpcm).
b) Tương tự câu a, CH,DF cũng cắt nhau tại 1 điểm trên (O), gọi nó là T
Dễ thấy AH = AS = AT (Tính chất đối xứng). Mà AH,AS,AT lần lượt là khoảng cách từ A đến EF,DE,DF
Nên A chính là tâm bàng tiếp góc D của \(\Delta\)DEF (A nằm ngoài \(\Delta\)DEF) (đpcm).
c) Gọi IH cắt CF tại G. Ta sẽ chỉ ra rằng B,G,E thẳng hàng. Thật vậy:
Ta có FA,FI là phân giác trong và ngoài của ^DFE => FI vuông góc AB => FI // CH
Từ đó \(\Delta\)IGF ~ \(\Delta\)HGC (g.g) => \(\frac{GI}{GH}=\frac{IF}{HC}\)(3)
Mặt khác ^IFE = ^FAH (Cùng phụ ^AFH) = ^HCB. Tương tự ^IEF = ^HBC
Suy ra \(\Delta\)EIF ~ \(\Delta\)BHC (g.g) => \(\frac{IF}{HC}=\frac{IE}{HB}\)(4)
Từ (3) và (4), kết hợp với ^GIE = ^GHB suy ra \(\Delta\)GEI ~ \(\Delta\)GBH (c.g.c)
=> ^IGE = ^HGB. Vì I,G,H thẳng hàng nên kéo theo B,G,E thẳng hàng
Vậy thì BE,CF,IH cắt nhau tại G (đpcm).
Bạn ơi, chứng minh cho mình câu b: AH=AS=AT với được không ạ