Cho a và b là hai số thực dương thỏa mãn điều kiện: a2006 +b2006= a2007 +b2007 = a2008 + b2008. Hãy tính tổng S= a2009 + b2009
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 10 2019
Đáp án A
Giá trị nhỏ nhất đạt được khi a = b = 2 . Vậy S = 3 a + b = 8 .
20 tháng 3 2023
Đặt a/b=b/c=c/a=k
=>a=bk; b=ck; c=ak
=>a=bk; b=ak*k=ak^2; c=ak
=>a=ak^3; b=ak^2; c=ak
=>k=1
=>a=b=c
\(B=\dfrac{a^{2022}\cdot a^{2023}}{a^{4045}}=1\)
DL
23 tháng 4 2018
Ta có: \((a^{2007}+b^{2007})\left(a+b\right)-\left(a^{2006}+b^{2006}\right)ab\)
\(=\left(a^{2008}+a^{2007}b+ab^{2007}+b^{2008}\right)-\left(a^{2007}b+ab^{2007}\right)\)
\(=a^{2008}+b^{2008}\)
Mà: \(a^{2006}+b^{2006}=a^{2007}+b^{2007}=a^{2008}+b^{2008}\) ( * )
\(\Rightarrow\left(a^{2008}+b^{2008}\right)\left(a+b\right)-\left(a^{2008}+b^{2008}\right)ab=a^{2008}+b^{2008}\)
\(\Leftrightarrow\left(a^{2008}+b^{2008}\right)\left(a+b-ab\right)=a^{2008}+b^{2008}\)
\(\Leftrightarrow a+b-ab=1\)
\(\Leftrightarrow\left(a-1\right)-b\left(a-1\right)=0\)
\(\Leftrightarrow\left(a-1\right)\left(1-b\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}\)
thay vào (*) ta tính dc:
a=1 thì\(\orbr{\begin{cases}b=1\\b=0\end{cases}}\) b=1 thì \(\orbr{\begin{cases}a=1\\a=0\end{cases}}\)
mặt khác a, b dương => a=1, b=1
Khi đó: \(a^{2009}+b^{2009}=1+1=2\)
23 tháng 4 2018
Ta có : \(a^{2006}+b^{2016}=a^{2007}+b^{2007}=a^{2008}+b^{2008}\)
\(\Leftrightarrow\orbr{\begin{cases}a^{2006}+b^{2006}-\left(a^{2007}+a^{2007}\right)=0\left(1\right)\\a^{2008}+b^{2008}-\left(a^{2007}+b^{2007}\right)=0\left(2\right)\end{cases}}\)
Cộng (1) với (2) => \(a^{2008}+b^{2008}-2\left(a^{2007}+b^{2007}\right)+a^{2006}+b^{2006}=0\)
\(\Leftrightarrow a^{2008}-2a^{2007}+a^{2006}+b^{2008}-2b^{2007}+b^{2006}\)
\(\Leftrightarrow a^{2006}\left(a^2-2a+1\right)+b^{2006}\left(b^2-2b+1\right)=0\)
\(\Leftrightarrow a^{2006}\left(a-1\right)^2+b^{2006}\left(b-1\right)^2=0\) (*)
Vì a , b > 0 và : \(\left(a-1\right)^2\ge0\forall a\) ; \(\left(b-1\right)^2\ge0\forall b\)
Nên : phương trình (*) <=> \(\hept{\begin{cases}\left(a-1\right)^2=0\\\left(b-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}a-1=0\\b-1=0\end{cases}\Leftrightarrow a=b=1}}\)
Vậy \(S=a^{2009}+b^{2009}=1+1=2\)
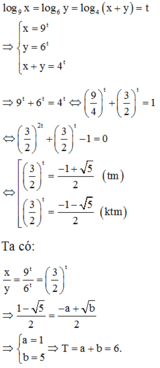
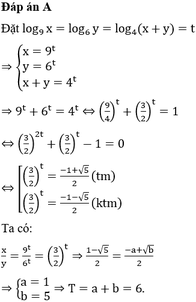
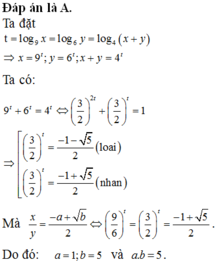
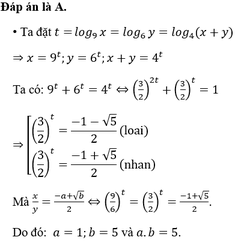
Ta có:
\(a^{2006}+a^{2008}+b^{2006}+b^{2008}\ge2\left(a^{2007}+b^{2007}\right)\)
Dấu = xảy ra khi \(a=b=1\)
\(\Rightarrow S=a^{2009}+b^{2009}=2\)