Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
chưa chị nhưng em đã biết rồi nên chị mà biết thì chỉ cho e
\(\text{#TNam}\)
`a,` Xét Tam giác `AMB` và Tam giác `EMC` có:
`MA=ME (g``t)`
\(\widehat{AMB}=\widehat{CME} (\text {2 góc đối đỉnh})\)
`MB=MC (\text {M là trung điểm của BC})`
`=> \text {Tam giác AMB = Tam giác EMC (c-g-c)}`
`b,` Vì Tam giác `AMB =` Tam giác `EMC (a)`
`-> AB = CE (\text {2 cạnh tương ứng}) (1)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`\text {BH chung}`
`=> \text {Tam giác ABH = Tam giác DBH (c-g-c)}`
`-> AB = BD (\text {2 cạnh tương ứng}) (2)`
Từ `(1)` và `(2) -> CE = BD.`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`\text {MH chung}`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HA = HD (g``t)`
`=> \text {Tam giác AMH = Tam giác DMH (c-g-c)}`
`-> MA = MD (\text {2 cạnh tương ứng})`
Xét Tam giác `AMD: MA = MD`
`-> \text {Tam giác AMD cân tại M}`
*Hoặc nếu như bạn có học rồi, thì mình có thể dùng cái này cũng được nè cậu:>.
Vì `MH` vừa là đường cao (hạ từ đỉnh `->` cạnh đối diện), vừa là đường trung tuyến.
Theo tính chất của tam giác cân `-> \text {Tam giác AMD là tam giác cân} (đpcm).`
a: Xét ΔAMB và ΔEMC có
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
=>ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔMAD có
MH vừa là đường cao, vừa là trung tuyến
=>ΔMAD cân tại M
a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)
a: Xét ΔAMB và ΔEMC co
MA=ME
góc AMB=góc EMC
MB=MC
=>ΔAMB=ΔEMC
b: Xet ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BD=BA=CE
c: Xét ΔAMD có
MH vừa là đường cao, vừa là trung tuyến
nên ΔAMD cân tại M
`\color {blue} \text {_Namm_}`
Mình xp sửa đề: Cho Tam giác `ABC (AB<AC)` (chứ nếu để vậy sẽ bị sai lệch thông tin của hình ;-;;)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = EM (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB=MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB=CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{AHB}=\widehat{DHB}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`-> AB=BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD=CE`
a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).
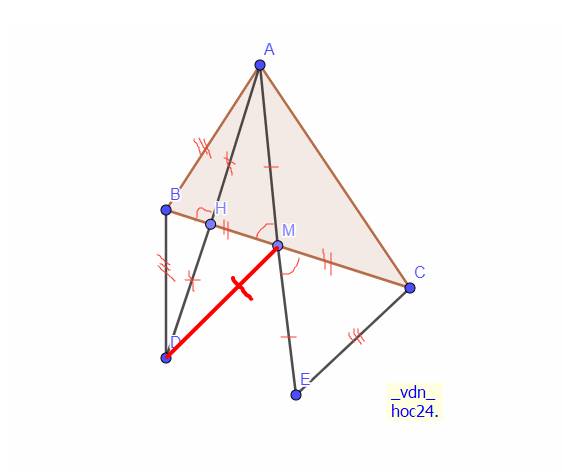
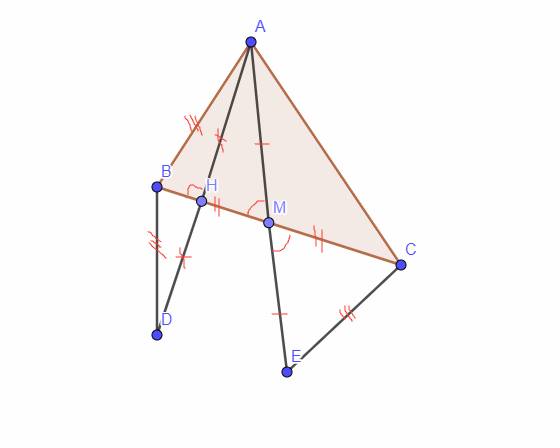
Hình tự vẽ
a,\(\Delta AMB\)và \(\Delta DMC\)có:
AM = DM (gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
MB = MC (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\)(2 góc tương ứng)
\(\Rightarrow AB//CD\)( vì có cặp góc so le trong bằng nhau )
b,hơi sai sai bn ơi