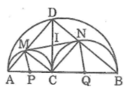
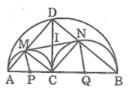
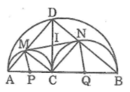
Cho đoạn thẳng AB, điểm C nằm giữa A và B. Vẽ về 1 phía AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, CB. Đường vuông góc với AB tại C cắt nửa đường tròn lớn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, CB theo thứ tự tại M, N
a, tứ giác DMCN là hình gì? Tại sao?
b, CM: DM.DA= DN. DB
c, CM: MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC và CB
d, Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất

 =
= 
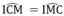 (6)
(6)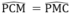 (7)
(7)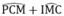 =
90
°
(8)
=
90
°
(8)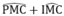 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM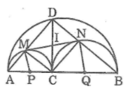


a: Xét (AB/2) có
ΔDAB nội tiếp
AB là đường kính
Do đó: ΔDAB vuông tại A
Xét (CA/2) có
ΔAMC nội tiếp
AC là đường kính
Do đó: ΔAMC vuông tại M
Xét (CB/2) có
ΔCNB nội tiếp
CB là đường kính
Do đó: ΔCNB vuông tại N
Xét tứ giác DMCN có
góc DMC=góc DNC=góc MDN=90 độ
nên DMCN là hình chữ nhật
b:DM*DA=DC^2
DN*DB=DC^2
Do đó: DM*DA=DN*DB