hai đường tròn tâm O và O'tiếp xúc với nhau tại A ( A nằm diua74 O và O'). Kẻ đường thẳng qua A cắt (O) ở C và cắt (O') ở B. Chứng minh OC//O'B
Vẽ dùm mình cái hình này đi!!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tóm tắt thôi nhé
a) Các cạnh // => Hình bình hành
T/g OBE = t/g OCD (^B=^C=90*, OB=OC, ^BOE=^COD vì cùng phụ với EOD) => OE = OD (2 cạnh kề) => Hình thoi
b) Nối OO' => 2 tam giác cân cùng góc đáy => so le trong => //
c) 1] OO' là đường trung trực của AB => đường trung bình
2] CB//OO'
Cm tương tự 1] để được BD//OO' => Ơ-clit => thẳng hàng

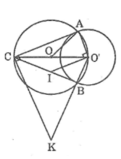
Trong đường tròn (O’) ta có AC và BC là hai tiếp tuyến cắt nhau tại C
Suy ra: ![]() (tính chất hai tiếp tuyến cắt nhau)
(tính chất hai tiếp tuyến cắt nhau)
Mà O’I ⊥ O’A (gt)
CA ⊥ O’A (chứng minh trên)
Suy ra: O’I // CA => ![]() (hai góc so le trong)
(hai góc so le trong)
Suy ra: ![]()
Hay tam giác CIO’ cân tại I => IC = IO’
Khi đó I nằm trên đường trung trực của O’C
Lại có: ![]() (tính chất hai tiếp tuyến cắt nhau)
(tính chất hai tiếp tuyến cắt nhau)
KC ⊥ CA (gt)
O’A ⊥ AC (chứng minh trên)
Suy ra: KC // O’A => ![]() (hai góc so le trong)
(hai góc so le trong)
Suy ra: ![]()
Hay tam giác CKO’ cân tại K => KC = KO’
Khi đó K nằm trên đường trung trực của O’C
Mặt khác: OC = OO’ (= R)
Suy ra O, I, K nằm trên đường trung trực của O’C
Vậy O, I, K thẳng hàng.
A1 =A2 đối đỉnh
Mà A1 =C; A2 =B (góc ở đáy tam giác cân)
=>B= C mà 2 góc này SLT => O'B//OC