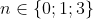Cho N biết (N +5) chia hết cho (N +1)
Giúp tui vs nhoa...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
1
25 tháng 2 2022
\(n-5⋮n+1\Leftrightarrow n+1-6⋮n+1\Rightarrow n+1\inƯ\left(-6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| n+1 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| n | 0 | -2 | 1 | -3 | 2 | -4 | 5 | -7 |
KK
1 tháng 6 2023
N chia 5 dư 3 => y là 3 hoặc 8
mà N chia 2 dư 1 => y là 3
N chia hết cho 9 , khi đó: 3 + x + 5 + 3 chia hết 9 <=> 11 + x chia hết 9
=> x = 7
Vậy N: 3753
BD
1 tháng 6 2023
\(N\div2\) (dư 1) \(\Rightarrow N\) là số lẻ \(\Rightarrow y\left\{1;3;5;7;9\right\}\)
\(N\div5\) (dư 3) \(\Rightarrow y\in\left\{3;8\right\}\). Nhưng vì N là số lẻ => y = 3
Vậy ta có số mới là: \(\overline{3x53}\)
\(N⋮9\Rightarrow3+x+5+3=\left(11+x\right)⋮9\Rightarrow x=7\\ \Rightarrow N=3753\)
GL
4
18 tháng 11 2019
https://olm.vn/hoi-dap/detail/69281920575.html
https://olm.vn/hoi-dap/detail/203933730813.html
https://olm.vn/hoi-dap/detail/85679676073.html
..........đây là một số link có câu hỏi tương tự như (n + 5) chia hết cho (n - 1)
#Học tốt!!!
M
18 tháng 11 2019
TL :
Ta có :
\(n+5⋮n+1\)
\(\Rightarrow n+1+4⋮n+1\)
\(\Rightarrow4⋮n+1\)( Vì n + 1 \(⋮\)cho n + 1 )
Mà : \(Ư\left(4\right)=\left\{1;2;4\right\}\)
\(TH1:\)
\(n+1=1\)
\(\Rightarrow n=1-1\)
\(\Rightarrow n=0\)
\(TH2:\)
\(n+1=2\)
\(\Rightarrow n=2-1\)
\(\Rightarrow n=1\)
\(TH3:\)
\(n+1=4\)
\(\Rightarrow n=4-1\)
\(\Rightarrow n=3\)
Vậy \(x\in\left\{0;1;3\right\}\)
KT
2
6 tháng 1 2016
10x+23 chia het cho 2x+1
=>5(2x+1)+18 chia het cho 2x+1
5(2x+1) chia het cho 2x+1
=>18 chia het cho 2x+1
=>2x+1 thuoc Ư(18)={1;2;3;6;9;18}
voi 2x+1=1=>x=0
voi 2x+1=2=>(loai)
voi 2x+1=3=>x=1
voi 2x+1=6=>(loai)
voi 2x+1=9=>x=4
voi 2x+1=18=>(loai)
vay x={0;1;4}
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
20 tháng 10 2021
a/
(n+1) và (n+2) là hai số TN liên tiếp nên chắc chắn 1 trong 2 số phải là số chẵn nên tích chia hết cho 2
b/
+ Nếu n chẵn => n+1 và n+5 lẻ => tích của chúng lẻ không chia hết cho 2
+ Nếu n lẻ => n+1 và n+5 chẵn => tích của chúng chẵn nên chia hết cho 2
=> (n+1)(n+5) chia hết cho 2 với mọi n lẻ
9 tháng 8 2015
a) n - 6 chia hết cho n-1
n - 1 - 5 chia hết cho n - 1
n - 1 thuộc U(-5)
Rồi bạn liệt kê ra
30 tháng 5 2017
a) n -6 chia hết cho n-1
n-1-5 chia hết cho n -1
n-1 chia hết cho n-1
=> n-1 € Ư (5)={1;5;-1;-5}
+ n-1 =1=>n=2
+n-1=5=>n=6
+n-1=-1=>n=0
+n+1=-5=>n=-4
=>n={2;6;0;-4}
10 tháng 10 2018
2n + 3 ⋮ n + 5
=> 2n + 10 - 7 ⋮ n + 5
=> 2(n + 5) - 7 ⋮ n + 5
2(n + 5) ⋮ n + 5
=> 7 ⋮ n + 5
=> n + 5 ∈ Ư(7) = {-1; 1; -7; 7}
=> n thuộc {-6; -4; -12; 2}
vậy_
b tương tự
n + 5 chia het cho n + 1
=> n + 1 + 4 chia het cho n + 1
Vi n + 1 chia het cho n + 1 nen de n + 1 + 4 chia het cho n + 1 thi 4 chia het cho n + 1
=> n + 1 thuoc uoc ( 4 )
=> n + 1 thuoc { 1 ; 2 ; 4 }
=> n thuoc { 0 ; 1 ; 3 }
Ta có :
Mà : Ư(4) =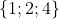
*TH1 :
* TH2:
* TH3:
Vậy :