Cho tam giác ACD. Vẽ cung tròn tâm A bán kính bằng CD, vẽ cung tròn tâm D bán kính bằng CA, chúng cắt nhau tại B( C và B nằm khác phía đối với AD). Chứng minh rằng AC//BD
viết có cả lời giải đáp nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC và ΔCDA, ta có:
AB = CD (theo cách vẽ)
AC cạnh chung
BC = AD (theo cách vẽ)
Suy ra: ΔABC = ΔCDA (c.c.c) ⇒ ∠(ACB) =∠(CAD) (hai góc tương ứng)
Vậy AD // BC ( vì có cặp góc so le trong bằng nhau)
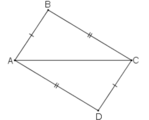

Mong các bạn giải nhanh giúp mình. Mai mình phải đi học rùi!!!!![]()
Mik ko ghi Gt và KL nhá
\(\Delta ACD\)và \(\Delta DBA\)có:
AC = BD (theo gt)
AB = CD (theo gt)
AD: cạnh chung
Do đó: \(\Delta ACD\)= \(\Delta DBA\)(c.c.c)
Suy ra: \(\widehat{A_1}=\widehat{D_1}\)(cặp góc tương ứng)
Mà hai góc này ở vị trí so le trong
Nên \(AC//BD\)(theo DHNB hai đường thẳng song song) (đpcm)