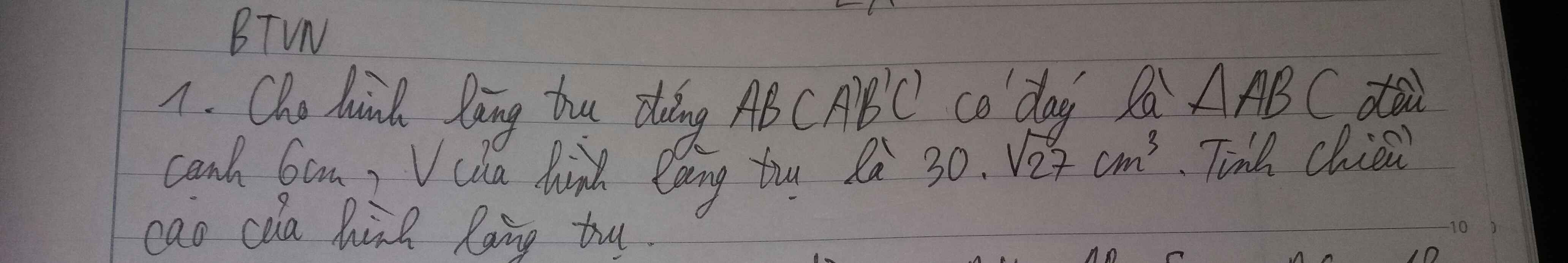Ai giúp mik bài này với, mik đang cần gấp lắm!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


c: \(=\dfrac{-27\cdot100}{-30}=\dfrac{2700}{30}=90\)


Bài 1
a, Có thể lập xy=21 <=> x=3;y=7 hoặc x=-3;y=-7
<=> x=7;y=3 hoặc x=-7;y=-3 ....v..v...
b, \(\left(x+5\right)\left(y-3\right)=15\)
\(\Rightarrow\orbr{\begin{cases}x+5=15\\y-3=15\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\y=18\end{cases}}}\)
c, \(\left(2x-1\right)\left(y-3\right)=12\)
\(\Rightarrow\orbr{\begin{cases}2x-1=12\\y-3=12\end{cases}\Rightarrow\orbr{\begin{cases}2x=13\\y=15\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{13}{2}\\y=15\end{cases}}}\)
Bài 2
Ư(6)={1;2;3;6} => 1+2+3+6=12
Ư(8)={1;2;4;8} => 1+2+4+8 =15
=> Tổng 2 ước này đều \(⋮3\)
๖²⁴ʱミ★Šїℓεŋէ❄Bʉℓℓ★彡⁀ᶦᵈᵒᶫ mù mắt =)) t làm mẫu câu b thôi, c nhìn vào mà làm
b) \(\left(x+5\right)\left(y-3\right)=15\)
\(\Rightarrow y-3=\frac{15}{x+5}\Rightarrow y=3+\frac{15}{x+5}\)
\(\Rightarrow x+5\inƯ\left(15\right)\)
Ta có: \(Ư\left(15\right)=\left\{-15;-5;-3;-1;0;1;3;5;15\right\}\)
\(x=\left\{0;-10;-8;-6;-20;-4;-2;0;10\right\}\)
Vì \(x\inℕ\Rightarrow x=\left\{0;10\right\}\)
\(\Rightarrow y=\left\{6;4\right\}\)
Vậy: (x,y) = {(0;10); (6;4)}

Ánh sáng yếu lắm , với cả chữ hơi khó đọc , hay viết tắt , nếu chứ khó đọc thì hãy viết mực xanh nhìn sáng với cả dễ đọc hơn nhiều đó bn .viết lại đi nếu biết mik trả lời cho nha okay !

em tán thành
vì Kỉ luật tạo nên sự đoàn kết, thống nhất, đảm bảo dân chủ được thực hiện một cách tốt nhất.
Có tinh thần, trách nhiệm trong học tập và công việc, luôn có ý thức vì tập thể.
"Có tinh thần, trách nhiệm trong học tập và công việc, luôn có ý thức vì tập thể." cái này là của câu b hả bạn

\(\left(xy+3\right)^2+\left(x+y\right)^2=8\)
\(\Leftrightarrow x^2y^2+x^2+y^2+1=-8xy\)
\(\dfrac{x}{x^2+1}+\dfrac{y}{y^2+1}=-\dfrac{1}{4}\Leftrightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{x^2y^2+x^2+y^2+1}=-\dfrac{1}{4}\)
\(\Rightarrow\dfrac{\left(xy+1\right)\left(x+y\right)}{-8xy}=-\dfrac{1}{4}\)
\(\Rightarrow\left(xy+1\right)\left(x+y\right)=2xy\)
\(\Rightarrow x+y=\dfrac{2xy}{xy+1}\)
Thế vào pt ban đầu:
\(\left(xy+3\right)^2+\left(\dfrac{2xy}{xy+1}\right)^2=8\)
Đặt \(xy+1=t\Rightarrow\left(t+2\right)^2+4\left(\dfrac{t-1}{t}\right)^2=8\)
\(\Rightarrow\left(t^2+2t\right)^2-4\left(t^2+2t\right)+4=0\)
\(\Leftrightarrow\left(t^2+2t-2\right)^2=0\)
\(\Rightarrow\left[{}\begin{matrix}t=-1-\sqrt{3}\\t=-1+\sqrt{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}xy=-2-\sqrt{3}\Rightarrow x+y=1+\sqrt{3}\\xy=-2+\sqrt{3}\Rightarrow x+y=1-\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow x;y\) là nghiệm của: \(\left[{}\begin{matrix}X^2-\left(1+\sqrt{3}\right)X-2-\sqrt{3}=0\\X^2-\left(1-\sqrt{3}\right)X-2+\sqrt{3}=0\end{matrix}\right.\)
\(\Rightarrow...\)