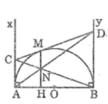
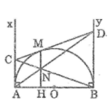
Cho đường tròn đường kính AB vẽ các tiếp tuyến Ax,By từ M trên đường tròn( M khác A,B) vẽ tiếp tuyến thứ 3 nó cắt Ax ở C cắt By ở D gọi N là giao điểm của BC và AO. Chứng minh rằng:
a,\(\dfrac{CN}{AC}=\dfrac{NB}{BD}\)
b,\(MN\perp AB\)
c,\(\widehat{COD}=90^o\)

a: Xét ΔNCA và ΔNBD co
góc NCA=góc NBD
góc CNA=góc BND
Do đó: ΔNCA đồng dạng với ΔNBD
=>NC/NB=NA/ND
=>NC/NA=NB/ND
c: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên OD là phân giác của góc MOB(2)
Từ (1) và (2) suy ra góc COD=1/2*180=90 độ