Giải dùm em câu 8 ạ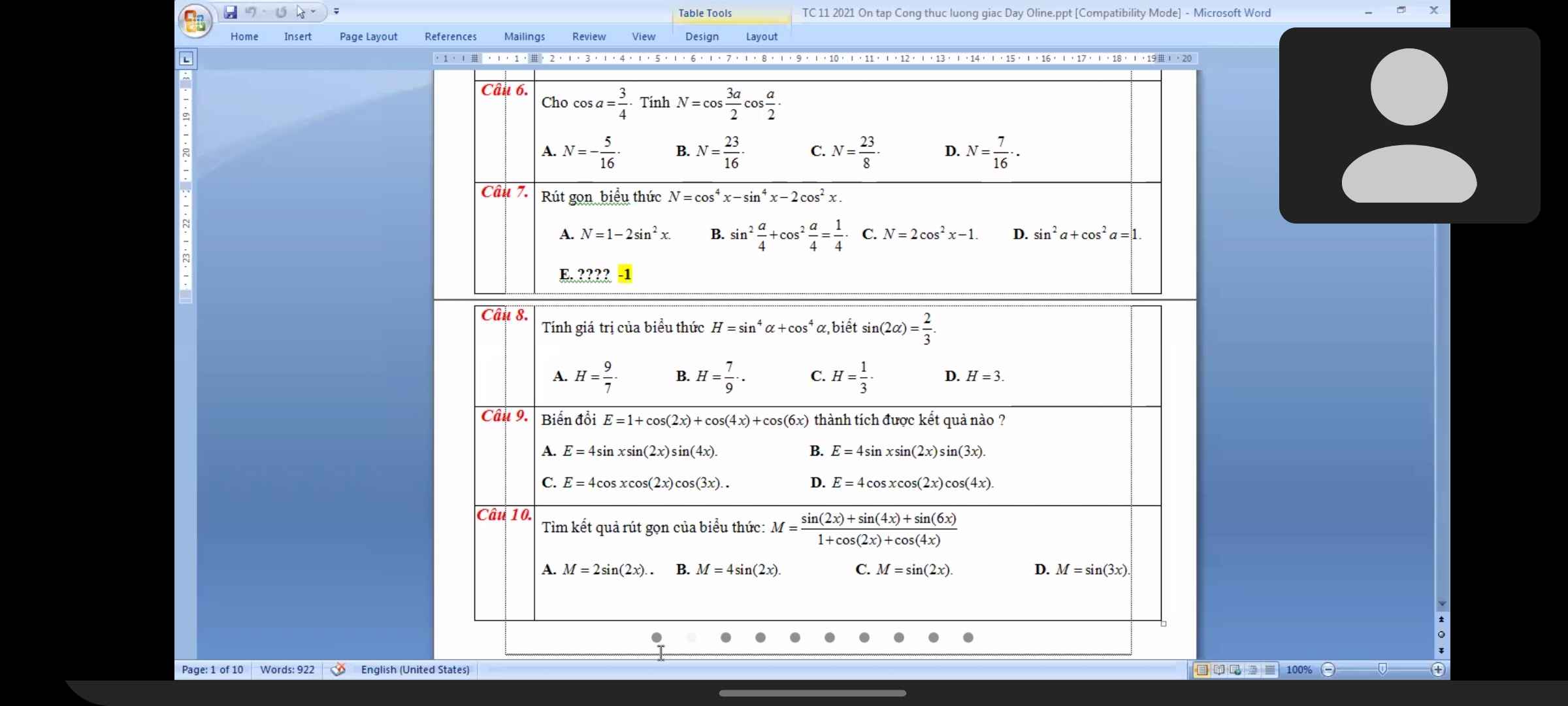
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
AH
Akai Haruma
Giáo viên
13 tháng 4 2021
2)
Đổi 1h15 phút thành 1,25 h
Thời gian dự định là: $\frac{AB}{40}$ (h)
Thời gian thực tế: $\frac{AB}{40-15}=\frac{AB}{25}$ (h)
Chênh lệch thời gian dự định và thời gian thực tế là:
$\frac{AB}{25}-\frac{AB}{40}=1,25$
$\frac{3AB}{200}=1,25\Rightarrow AB=83,33$ (km)
AH
Akai Haruma
Giáo viên
13 tháng 4 2021
Câu 3:
Đổi 20 phút thành $\frac{1}{3}$ giờ
Giả sử sau khi ô tô đi được $a$ giờ thì hai xe gặp nhau tại $C$. Lúc này, xe máy đã đi được $a+\frac{1}{3}$ giờ
Ta có:
$AC=35(a+\frac{1}{3})=(35+20).a$
$\Leftrightarrow 35(a+\frac{1}{3})=55a$
$\Rightarrow a=\frac{7}{12}$ (h)
Đổi $\frac{7}{12}$ h = 35 phút. Vậy sau khi đi được 35 phút thì ô tô gặp xe máy.
4 tháng 9 2021
Câu 34:
|vmax| = A.ω = 31,4 (cm/s) \(\Rightarrow\) A = \(\dfrac{\left|v_{max}\right|}{\omega}\)
Ta có công thức: vmin = \(\dfrac{S_{min}}{\Delta t}\)(*)
vì Δt < \(\dfrac{T}{2}\) (\(\dfrac{T}{6}\) < \(\dfrac{T}{2}\))
\(\Rightarrow\)Smin = 2.A. (1 - cos \(\dfrac{\Delta\phi}{2}\)) (Δϕ là góc ở tâm mà bán kính quét được qua khoảng thời gian Δt ấy, có công thức: Δϕ = ω. Δt)
Mấu chốt của bài này là bạn phải đưa biểu thức (*) về chỉ còn một ẩn là |vmax| thôi nhé! (Sử dụng công thức ω = \(\dfrac{2\pi}{T}\) để rút gọn)
(*) \(\Leftrightarrow\) vmin = \(\dfrac{2.A.\left[1-cos\left(\dfrac{\omega.\Delta t}{2}\right)\right]}{\Delta t}\)
\(\Leftrightarrow\) vmin = \(\dfrac{2.\dfrac{\left|v_{max}\right|}{\omega}.\left[1-cos\left(\omega.\dfrac{T}{6.2}\right)\right]}{\dfrac{T}{6}}\) (ở bước này là mình thay các biểu thức trên kia vào nhé)
\(\Leftrightarrow\) vmin = \(\dfrac{2.\left|v_{max}\right|\left[1-cos\left(\dfrac{2\pi}{T}.\dfrac{T}{12}\right)\right]}{\dfrac{T}{6}.\dfrac{2\pi}{T}}\)
Giờ thì ngồi rút gọn T thôi nào!
\(\Leftrightarrow\) vmin = \(\dfrac{2\left|v_{max}\right|.\left(1-cos\dfrac{\pi}{6}\right)}{\dfrac{\pi}{3}}\)
Thay |vmax| = 31,4 và π = 3,14. *Lưu ý là cos \(\dfrac{\pi}{6}\) = \(\dfrac{\sqrt{3}}{2}\) luôn nha (đừng thay π = 3,14 vào đấy!)
\(\Rightarrow\) vmin = \(\dfrac{6.31,4.\left(1-\dfrac{\sqrt{3}}{2}\right)}{3,14}\) = 8,038475773... (cm/s) \(\approx\) 8,04 (cm/s)
Vậy đáp án cần tìm là A. 8,04 cm/s
Có gì thắc mắc cứ hỏi nha. Chúc bạn học tốt!
HT
9 tháng 3 2021
Gọi G là trọng tâm tam giác ABC
\(\overrightarrow{A'A}+\overrightarrow{B'B}+\overrightarrow{C'C}=\overrightarrow{0}\Leftrightarrow\overrightarrow{A'G}+\overrightarrow{GA}+\overrightarrow{B'G}+\overrightarrow{GB}+\overrightarrow{C'G}+\overrightarrow{GC}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}=\overrightarrow{0}\)
Goi G la trong tam tam giac A'B'C'
Lai co: \(\overrightarrow{G'A'}+\overrightarrow{G'B'}+\overrightarrow{G'C'}=\overrightarrow{0}\)
\(\Rightarrow G'\equiv G\Rightarrow G'=\left(1;0;-2\right)\)
KN
0
giải dùm em câu 4 vợi ạ 
Lời giải:
$H=(\sin ^2a+\cos ^2a)^2-2\sin ^2a\cos ^2a$
$=1-\frac{1}{2}(2\sin a\cos a)^2=1-\frac{1}{2}(\sin 2a)^2=1-\frac{2}{9}=\frac{7}{9}$
Đáp án B.