Cho hình thoi ABCD . Trên tia đối của tia BA lấy M,trên tia đối của CB lấy N,trên tia đối của DC lấy P,trên tia đối của AD lấy Q sao cho BM=CN=DP=AQ
a) CM tứ giác MNPQ và BMPQ là hình bình hành
b) CM ABCD và MNPQ có chung tâm đối xứng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 3 2018
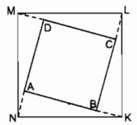
Xét △ ANK và △ BKL :
AN = BK (gt)
∠ A = ∠ B = 90 0
AK = BL (vì AB = BC, BK = CL)
Do đó △ ANK = △ BKL (c.g.c)
⇒ NK = KL (1)
Xét △ BKL và △ CLM:
BK = CL (gt)
∠ B = ∠ C = 90 0
BL = CM (vì BC = CD, CL = DM)
Do đó: △ BKL = △ CLM (c.g.c)
⇒ KL = LM (2)
Xét △ CLM và △ DMN :
CL = DM (gt)
∠ C = ∠ D = 90 0
CM = DN (vì CD = DA, DM = AN)
Do đó: △ CLM = △ DMN (c.g.c)
⇒ LM = MN (3)
Từ (1), (2) và (3) ⇒ NK = KL = LM = MN
Tứ giác MNKL là hình thoi
△ ANK = △ BKL ⇒ ∠ (ANK) = ∠ (BKL)
Trong tam giác ANK có A là góc vuông ⇒ ∠ (ANK) + ∠ (AKN) = 90 0
⇒ ∠ (BKL) + ∠ (AKN) = 90 0 hay ∠ (NKL) = 90 0
Vậy tứ giác MNKL là hình vuông.
