Bài 1 : Cho tam giác ABC vuông góc tại A tia phân giacd B cắt AC tại D . Trên BC lấy điểm E sao cho : BE =BA
a) Vẽ hình viết giả thiết kết luận b)chứng minh DA=DE
b)trên tia dôid của tia AB lấy K sao cho AK =EC,Chứng minh DK=DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
5 tháng 5 2021
vì dùng máy tính nên ko vẽ hình đc thông cảm !!
a) giả thiết
Δ ABC cân tại A
AK là tia đối của AB
BK=BC
KH⊥BC(H∈BC)
KH cắt AC tại E
Kết luận
KH=AC
BE là tia phân giác của góc ABC
b) xét tam giác BAC và tam giác BHK có
\(\widehat{B} \) Chung
KH=BC (gt)
\(\widehat{BAC}=\widehat{BHK}=90\) (gt)
tam giác BAC = tam giác BHK (ch-gn)
=>KH=AC(2 góc tương ứng )
b)Xét Δ KBC có BK=BC(gt)
=> tam giác KBC cân tại B
Mà KH⊥BC=> KH là đường cao
AC⊥AB =>AC⊥KB(K∈AB)=>AC là đường cao
Mà AC giao vs KH tại E
=> E là trực tâm của tam giác
=> BE là đường cao (tc 3 đg cao trong tam giác)
=> BE là giân giác của góc \(\widehat{KBC}\)
=>BE là giân giác của góc \(\widehat{ABC} \) (A∈BK)
15 tháng 3 2021
a) Xét ΔDAB và ΔDEB có
BA=BE(gt)
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
BD chung
Do đó: ΔDAB=ΔDEB(c-g-c)
Suy ra: DA=DE(Hai cạnh tương ứng)
6 tháng 3 2023
`a)`
Có `BD` là p/g của `hat(ABC)(GT)=>hat(B_1)=hat(B_2)`
Xét `Delta ABD` và `DElta EBD` có :
`{:(BA=BE(GT),(hat(B_1)=hat(B_2)(cmt),(BD-chung):}}`
`=>Delta ABD=Delta EBD(c.g.c)(đpcm)`
`b)`
Có `Delta ABD=Delta EBD(cmt)=>hat(A)=hat(E_1)` ( 2 góc t/ứng )
mà `hat(A)=90^0`
nên `hat(E_1)=90^0(đpcm)`
6 tháng 3 2023
`\color {blue} \text {_Namm_}`
`a,`
Xét Tam giác `ABD` và Tam giác `EBD` có:
`BA=BE (g``t)`
\(\widehat{ABD}=\widehat{EBD}\) `(` tia phân giác \(\widehat{ABE}\) `)`
`BD` chung
`=>` Tam giác `ABD =` Tam giác `EBD (c-g-c)`
`b,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`->`\(\widehat{BAD}=\widehat{BED}\) `(2` góc tương ứng `)`
Mà góc \(\widehat{A}\) vuông `(`\(\widehat{A}=90^0\) `)`
`-> `\(\widehat{BAD}=\widehat{BED}=90^0\)
`c,` Vì Tam giác `ABD =` Tam giác `EBD (a)`
`-> DE=DA (2` cạnh tương ứng `)`
Xét Tam giác `DEC:`
\(\widehat{DEC}=90^0\) `-> DC` là cạnh lớn nhất `-> DC>DE`
Mà `DE=DA -> DC>DA`
5 tháng 3 2022
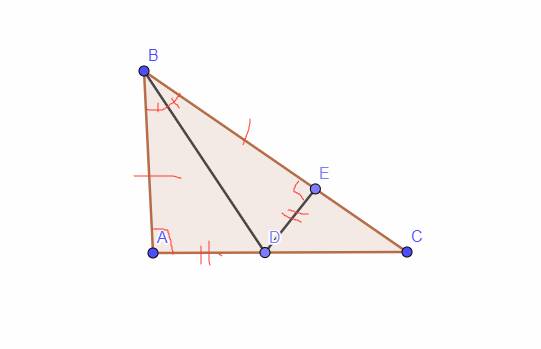
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: DK=DC
hay ΔDKC cân tại D
c: \(AC=\sqrt{BC^2-AB^2}=8\left(cm\right)\)
d: Ta có: DK=DC
mà DC>DE
nên DK>DE
5 tháng 1 2022
b: Ta có: ΔAIE cân tại A
mà AK là đường phân giác
nên K là trung điểm của EI
hay KE=KI
c: Xét ΔAID và ΔAED có
AI=AE
\(\widehat{IAD}=\widehat{EAD}\)
AD chung
Do đó: ΔAID=ΔAED
Suy ra: \(\widehat{AID}=\widehat{AED}=90^0\)
=>DE⊥AB
mà AC⊥AB
nên DE//AC
