Bạn sẽ giải thích thế nào nếu một hệ thống máy tính, khi trừ số thực dương nhỏ nhất khỏi số thực dương lớn nhất lại trả về số thực dương lớn nhất? Nói cách khác, máy tính thực hiện a - b, trong đó a là số thực lớn nhất và b là số thực dương nhỏ nhất. Kết quả là a. Làm thế nào mà có thể được? A. Không thể nào. Đó là một lỗi trong hệ thống. B. Đây là một trường hợp thiếu dòng và kết quả không chính xác. C. Đây là trường hợp tràn và kết quả không chính xác. D. Kết quả là chính xác. Số gần nhất với kết quả là a.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

uses crt;
var a,b:array[1..100]of real;
i,n,dem:integer;
max:real;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
dem:=0;
for i:=1 to n do
if a[i]>0 then
begin
inc(dem);
b[dem]:=a[i];
end;
if dem=0 then writeln('1')
else begin
max:=b[1];
for i:=1 to dem do
if max<b[i] then max:=b[i];
writeln(max:4:2);
end;
readln;
end.

a) Phép cộng và phép trừ
b) Phép trừ
c) Phép trừ, phép nhân và phép chia
a) Tập hợp các số hữu tỉ khác 0 tất cả các phép cộng, trừ, nhân , chia luôn thực hiện được
b) Tập hợp các số hữu tỉ dương : phép trừ không phải luôn thực hiện được
Ví dụ: (1/3) - (3/4) kết quả không phải là số hữu tỉ dương
c) Tập hợp các số hữu tỉ âm: phép trừ, nhân và chia không phải luôn luôn thực hiện được
Ví dụ: (-1/3) - (-3/4) kết quả không phải là số hữu tỉ âm

Tập hợp các số hữu tỉ dương : phép trừ không phải luôn thực hiện được
Ví dụ: (1/3) - (3/4) kết quả không phải là số hữu tỉ dương

b, Tập hợp các số hữu tỉ dương:
* Trừ: 1/1 - 111111/2356 = - 46,16086587 (*)
* Cộng: 1/1 + 111111/2356 = 48,16086587 (*)
* Chia: 123 : 456 = 0,269736842 (*)
c, Tập hợp các số hữu tỉ âm:
* Trừ: -1/1 - (-111111/2356) = 46,16086587 (*)
* Cộng: -1/1 + (-111111/2356) = - 48,16086587 (*)
* Chia: -123 : (-456) = 0,269736842 (*)
a, Tập hợp các số hữu tỉ khác 0 gồm tập hợp các số hữu tỉ dương và âm:
* Trừ, cộng, chia: VD ở trên

uses crt;
var a:array[1..100]of integer;
i,n,t,ln,nn:integer;
begin
clrscr;
readln(n);
for i:=1 to n do readln(a[i]);
t:=0;
for i:=1 to n do
if a[i]>0 then t:=t+a[i];
ln:=a[1];
nn:=a[1];
for i:=1 to n do
begin
if ln<a[i] then ln:=a[i];
if nn>a[i] then nn:=a[i];
end;
writeln(t);
writeln(ln);
writeln(nn);
readln;
end.

Đáp án C
Phương pháp:
Rút y theo x từ phương trình (1), thế vào phương trình (2) để tìm khoảng giá trị của x.
Đưa biểu thức P về 1 ẩn x và tìm GTLN, GTNN của biểu thức P.
Cách giải: 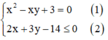
Ta nhận thấy x = 0 không thỏa mãn phương trình (1), do đó 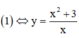 thế vào (2):
thế vào (2):
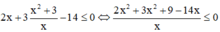
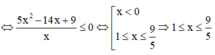
![]()
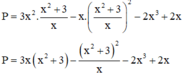
Sử dụng MTCT ta tính được
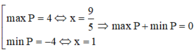
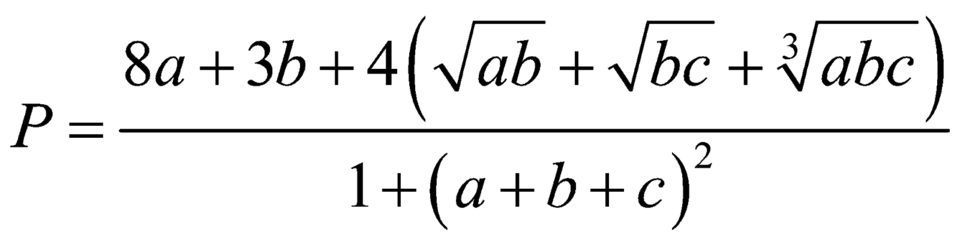
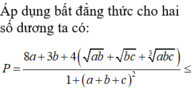
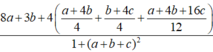
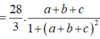
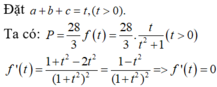
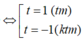
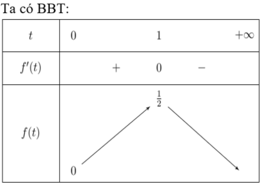

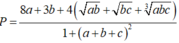 gần với giá trị nào nhất trong các đáp án sau:
gần với giá trị nào nhất trong các đáp án sau:
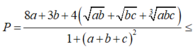
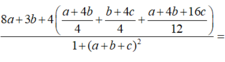
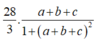
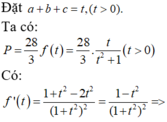
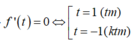
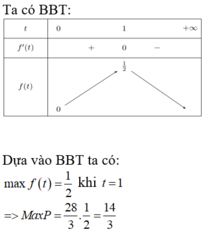
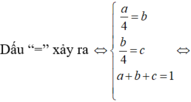
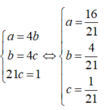
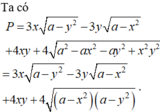
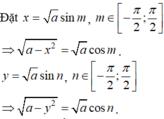

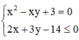 Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu
Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của biểu