Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A.
Xếp 12 học sinh thành 1 dãy có: 12! Cách sắp xếp.
Chọn 2 bạn nữ và sắp xếp 2 bạn đứng đầu hàng và cuối hàng có: 2 . C 7 2 cách.
Sắp xếp 10 bạn còn lại có: 10! Cách.
Do đó có: 2 C 7 2 . 10 ! cách sắp xếp 12 học sinh sao cho người đứng đầu hàng và cuối hàng đều là nữ.
Xác suất cần tìm là: P = 2 . C 7 2 . 10 ! 12 ! = 7 22
Chọn C
Chọn mỗi tổ hai học sinh nên số phần tử của không gian mẫu là 
Gọi biến cố A: “Chọn 4 học sinh từ 2 tổ sao cho 4 em được chọn có 2 nam và 2 nữ”
Khi đó, xảy ra các trường hợp sau:
TH1: Chọn 2 nam ở Tổ 1, 2 nữ ở Tổ 2. Số cách chọn là 
TH2: Chọn 2 nữ ở Tổ 1, 2 nam ở Tổ 2. Số cách chọn là 
.
TH3: Chọn ở mỗi tổ 1 nam và 1 nữ. Số cách chọn là 
Suy ra, n(A) = 
Xác suất để xảy ra biến cố A là: 
Đáp án A
Kí hiệu học sinh các lớp 12A, 12B, 12C lần lượt là A, B, C
Ta sẽ xếp 5 học sinh của lớp 12C trước, khi đó xét các trường hợp sau:
TH1: CxCxCxCxCx với x thể hiện là ghế trống. Khi đó, số cách xếp là 
cách.
TH2: xCxCxCxCxC giống với TH1=> có 
cách xếp.
TH3: CxxCxCxCxC với xx là hai ghế trống liền nhau.
Chọn 1 học sinh lớp 12A và 1 học sinh lớp 12B vào hai ghế trống đó => 
cách xếp.
Ba ghế trống còn lại ta sẽ xếp 3 học sinh còn lại của 2 lớp 12A-12B => 
cách xếp.
Do đó, TH3 có 
cách xếp.
Ba TH4. CxCxxCxCxC.
TH5. CxCxCxxCxC.
TH6. CxCxCxCxCxx tương tự TH3.
Vậy có tất cả 
cách xếp cho các học sinh.
Suy ra xác suất cần tính là
Chọn C
Số phần tử của không gian mẫu là 
Gọi A là biến cố "không có hai học sinh nữ nào đứng cạnh nhau".
Mỗi phần tử của A tương ứng với 1 hàng ngang gồm 11 bạn đã cho mà không có hai nữ xếp cạnh nhau. Để xếp được 1 hàng như vậy ta thực hiện liên tiếp hai bước:
Bước 1: Xếp 6 bạn nam thành một hàng ngang, có 6!= 720 cách
Bước 2: Xếp 5 bạn nữ vào 7 vị trí xen giữa hai nam hoặc ngoài cùng (để 2 nữ không cạnh nhau), có A 7 5 = 2520 cách.
Vậy n(A) =720.2520 = 1814400
Xác suất cần tìm là 
Đáp án C
Số cách xếp ngẫu nhiên là 10!.
Ta tìm số cách xếp thoả mãn:
Đánh số hàng từ 1 đến 10. Có hai khả năng:
5 nam xếp vị trí lẻ và 5 nữ xếp vị trí chẵn có 5! x 5! = 120 2 .
5 nam xếp vị trí chẵn và 5 nữ xếp vị trí lẻ có 5! x 5! = 120 2 .
Theo quy tắc cộng có 120 2 + 120 2 = 2 × 120 2 cách xếp thoả mãn.
Vậy xác suất cần tính 2 5 ! 2 10 ! = 1 126 .
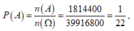
Lời giải:
Xếp $12$ học sinh gồm $7$ nam, $5$ nữ theo hàng dọc ta có \(12!\) cách xếp
Trươc tiên, chọn 1 bạn là nam đứng đầu hàng ta có $7$ cách chọn
Chọn 1 bạn nam đứng cuối hàng ta có $6$ cách chọn
$10$ bạn còn lại xếp ở bên trong ta có \(10!\) cách xếp
Do đó số kết cục thuận lợi: \(7.6.10!\)
Vậy xác suất để người đứng hàng đầu và cuối đều là nam là:
\(P(A)=\frac{7.6.10!}{12!}=\frac{7}{22}\)
Đáp án C