Tìm các số nguyên dương m,n thỏa mãn:2m-3n=7
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
19 tháng 12 2015
Trong một số trường hợp, có thể sử dụng mối quan hệ đặc biệt giữa ƯCLN, BCNN và tích của hai số nguyên dương a, b, đó là : ab = (a, b).[a, b], trong đó (a, b) là ƯCLN và [a, b] là BCNN của a và b. Việc chứng minh hệ thức này khụng khú :
Theo định nghĩa ƯCLN, gọi d = (a, b) => a = md ; b = nd với m, n thuộc Z+ ; (m, n) = 1 (*)
Từ (*) => ab = mnd2 ; [a, b] = mnd
=> (a, b).[a, b] = d.(mnd) = mnd2 = ab
=> ab = (a, b).[a, b] . (**)
9 tháng 9 2020
Đặt \(3n+6=x^3,n+1=y^3\)vì \(n\inℕ^∗\)nên \(x>1,y>3\)và x,y nguyên dương
\(\left(3n+6\right)-\left(n+1\right)=x^3-y^3\)
\(\Leftrightarrow2n+5=\left(x-y\right)\left(x^2+xy+y^2\right)\)(1)
Vì 2n+5 là số nguyên tố nên chỉ có 2 ước là 1 và 2n+5 mà (x-y) và (x2+xy+y2) cũng là 2 ước của 2n-5 nên:
\(\orbr{\begin{cases}x-y=1,x^2+xy+y^2=2n+5\\x^2+xy+y^2=1,x-y=2n+5\end{cases}}\)mà \(x>1,y>3\)nên vế dưới không thể xảy ra.
Vậy \(\hept{\begin{cases}x=y+1\\x^2+xy+y^2=2n+5\end{cases}}\)thay vế trên vào vế dưới\(\Rightarrow\left(y+1\right)^2+y\left(y+1\right)+y^2=2n+5\)
\(\Rightarrow3y^2+3y+1=2n+5\)
Vậy ta xét \(\hept{\begin{cases}3y^2+3y+1=2n+5\\y^3=n+1\Rightarrow2y^3=2n+2\end{cases}}\)trừ 2 biểu thức vế theo vế:
\(\Rightarrow-2y^3+3y^2+3y+1=3\Leftrightarrow\left(y+1\right)\left(y-2\right)\left(1-2y\right)=0\)
Vì nguyên dương nên nhận y=2--->n=7
DH
0
CM
25 tháng 9 2017
Viết ngược lại biểu thức của S, ta được
Cộng (1) và (2) vế theo vế và kết hợp với công thức 
ta có
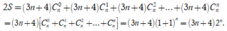
Theo giả thiết: 
Chọn B.
CM
8 tháng 11 2018
Đáp án B
Ta có: S = 2 C n 0 + ... + C n n + 3 C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Xét khai triển 1 + x n = C n 0 + C n 1 x + ... + C n n x n
Đạo hàm 2 vế ta có: n 1 + x n − 1 = C n 1 + 2 C n 2 x + 3 C n 3 x 2 + ... + n C n n x n − 1
Cho x = 1 ta có: 2 n = C n 0 + C n 1 + ... + C n n ; n .2 n − 1 = C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Do đó S = 2.2 n + 3. n 2 n − 1 = 1600 → S H I F T − C A L C n = 7.
CM
22 tháng 5 2017
Đáp án B
Ta có S = 2 C n 0 + ... + C n n + 3 C n 1 + 2 C n 2 + 3 C n 3 + .. + n C n n
Xét khai triển 1 + x n = C n 0 + C n 1 x + ... + C n n x n
Đạo hàm 2 vế ta có n 1 + x n − 1 = C n 1 + 2 C n 2 x + ... + n C n n x n − 1
Cho x = 1 ta có 2 n = C n 1 + 2 C n 2 + ... + C n n ; n 2 n − 1 = C n 1 + 2 C n 2 + 3 C n 3 + ... + n C n n
Do đó S = 2.2 n + 3. n .2 n − 1 = 1600 → S H I F T − C A L C n = 7
mình bieetslaf đúng nhưng cac pạn chỉ cho mình cách làm đc ko?mai mình phải nộp bài rồi