cho tam giác ABC, chứng minh cosA/2.cosB/2. cosC/2<=3 căn 3/8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
PT
1
29 tháng 10 2021
Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\
=\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\
=\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)
Y
24 tháng 7 2020
Ta chứng minh chiều nghịch:
Khi tam giác ABC đều, góc A=gócB=gócC=60*
Khi đó cosA+cosB+cosC=3/2(đpcm)
Ta chứng minh chiều thuận
Ta chứng minh cosA+cosB+cosC≤3/2
Thật vậy:
Mà theo gt, cosA+cosB+cosC=3/2
nên ta có tam giác ABC đều(đpcm)
24 tháng 7 2020
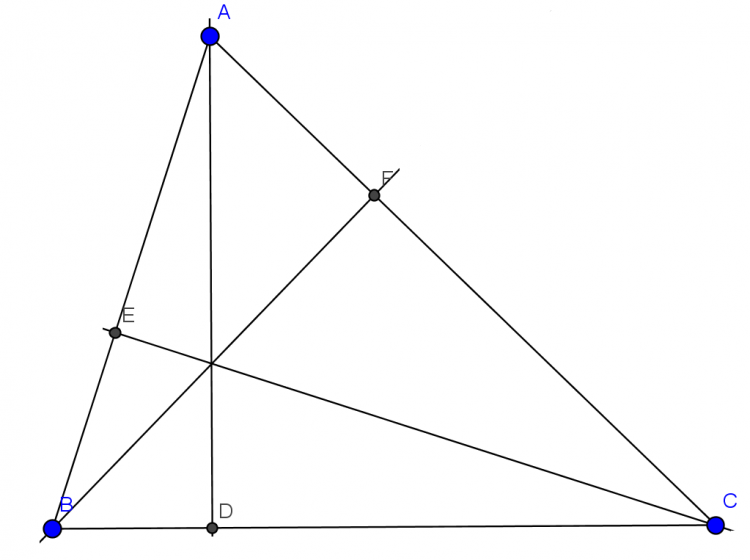
vẽ AD,BE, CF là các đường cao của tam giác ABC
\(\cos A=\sqrt{\cos BAE\cdot\cos CAF}=\sqrt{\frac{AE}{AB}\cdot\frac{AE}{AC}}=\sqrt{\frac{AF}{AB}\cdot\frac{AE}{AC}}\le\frac{1}{2}\left(\frac{AF}{AB}+\frac{AE}{AC}\right)\)
ta có \(\cos A\le\frac{1}{2}\left(\frac{AF}{AB}+\frac{AE}{AC}\right)\left(1\right)\)
tương tự \(\cos B\le\frac{1}{2}\left(\frac{BF}{AB}+\frac{BD}{BC}\right)\left(2\right);\cos C\le\frac{1}{2}\left(\frac{CD}{BC}+\frac{CE}{AC}\right)\left(3\right)\)
do đó \(\cos A+\cos B+\cos C\le\frac{1}{2}\left(\frac{AF}{AB}+\frac{AE}{AC}+\frac{BF}{AB}+\frac{BD}{BC}+\frac{CD}{BC}+\frac{CE}{AC}\right)\)
\(\Rightarrow\cos A+\cos B+\cos C\le\frac{1}{2}\left(\frac{AF}{AB}+\frac{BF}{AB}+\frac{AE}{AC}+\frac{CE}{AC}+\frac{BD}{BC}+\frac{CD}{BC}\right)\)
\(\Rightarrow\cos A+\cos B+\cos C\le\frac{3}{2}\)
dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\frac{AF}{AB}=\frac{AE}{AC}\\\frac{BF}{AB}=\frac{BD}{BC}\\\frac{CD}{BC}=\frac{CE}{AC}\end{cases}}\Leftrightarrow AB=AC=BC\)
do vậy cosA+cosB+cosC=3/2 <=> AB=AC=BC <=> tam giác ABC đều
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2021
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
2 tháng 3 2021
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
TV
1
NL
0
NT
0
TH
0
